👉 📐 Teorema dos Segmentos Tangentes: o segredo das tangentes iguais!
🟢 1️⃣ O que é o Teorema dos Segmentos Tangentes? 📐📏
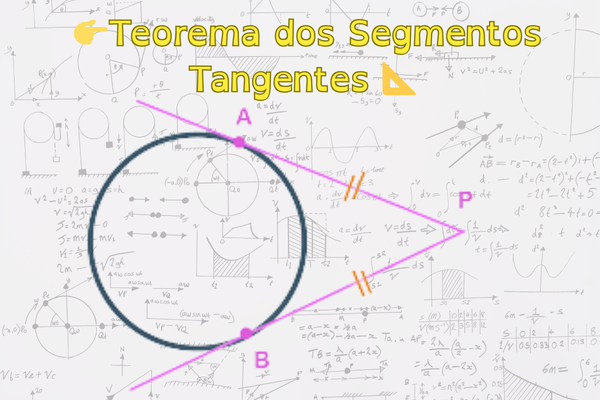
Imagine um ponto fora de uma circunferência, e a partir dele você traça duas retas que tocam o círculo exatamente em um ponto cada — formando dois segmentos retos até os pontos de tangência.
✨ Pois é: o que muita gente não sabe é que esses dois segmentos medem exatamente o mesmo comprimento.
Isso é o que chamamos de Teorema dos Segmentos Tangentes — uma das ideias mais elegantes e úteis da geometria plana!
🔹 📜 Enunciado do teorema:
👉 “Os segmentos tangentes traçados de um mesmo ponto externo a uma circunferência possuem comprimentos iguais.”
Em outras palavras:
📍 Se PA e PB são tangentes traçadas do ponto P até a circunferência, então:
PA = PB
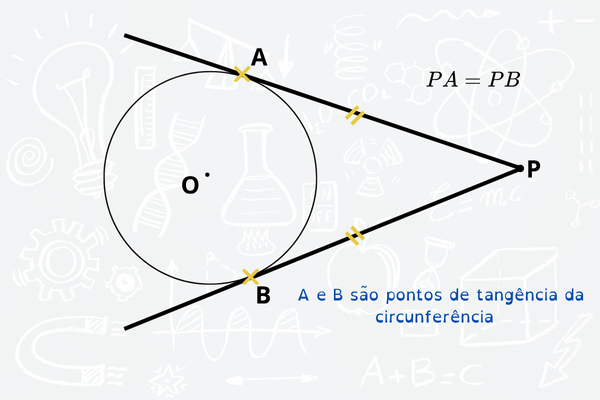
🔹 📏 Representação comum em provas:
Imagine uma circunferência com centro O e um ponto P fora dela.
Você traça dois segmentos:
- Um vai do ponto P até o ponto A na borda do círculo (PA)
- Outro do mesmo ponto P até o ponto B, também tangente ao círculo (PB)
📐 Como ambos tocam a circunferência em pontos distintos, mas vêm do mesmo ponto externo, temos:
PA = PB
Essa igualdade é certeira e aparece direto em questões de concursos militares, seja em forma de cálculo ou interpretação visual.
🔹 🔍 O que esse teorema resolve na prática?
- Facilita o cálculo de perímetros e distâncias.
- Ajuda a resolver triângulos com círculos inscritos ou circunscritos.
- Aparece em questões que exigem identificação de simetria ou igualdade de segmentos.
- Serve de base para aplicar o Teorema de Pitágoras em triângulos formados por tangentes.
2️⃣ Como identificar esse teorema em uma questão de prova
📌 Sinais visuais:
Procure sempre um ponto fora da circunferência (geralmente chamado de P) do qual saem duas retas tangentes tocando o círculo em dois pontos distintos (A e B). Essas tangentes costumam formar uma figura parecida com um “chapéu” ou um “V” aberto.
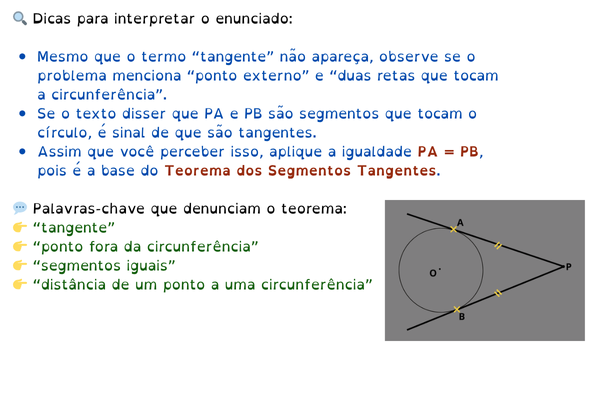
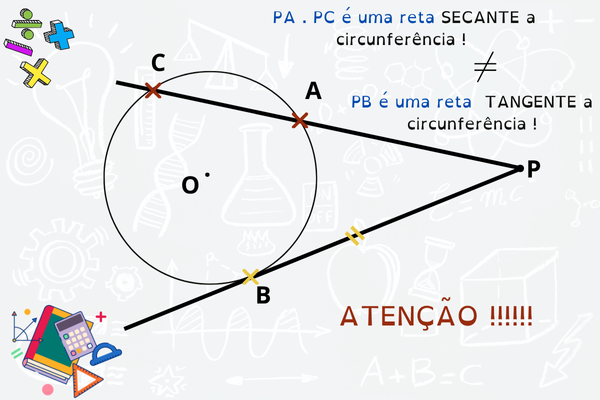
⚠️ Armadilhas comuns nas alternativas:
- Confundir tangente com secante (a tangente toca o círculo em um ponto; a secante atravessa em dois).
- Esquecer que os segmentos tangentes são iguais, mesmo quando o problema apresenta medidas diferentes para confundir.
- Tentar somar os comprimentos em vez de igualá-los (erro frequente).
- Ignorar que o ângulo entre o raio e a tangente é sempre de 90°.
🟢 3️⃣ Aplicações do Teorema em cálculos práticos
📏 1. Usando o teorema em problemas de perímetro, área e equações
O Teorema dos Segmentos Tangentes é muito útil quando o problema envolve comprimentos iguais saindo de um mesmo ponto externo.
➡️ Como PA = PB, basta igualar as expressões algébricas que representam os segmentos para encontrar valores desconhecidos.
🔹 Exemplo: se PA = x + 2 e PB = 3x − 4, então x + 2 = 3x − 4 → x = 3.
📐 2. Aplicação em triângulos circunscritos e figuras simétricas
Quando um triângulo é circunscrito a uma circunferência, cada lado é tangente em dois pontos.
Assim, as tangentes a partir de um mesmo vértice são iguais:
➡️ Se o triângulo é ABC e os pontos de tangência são D, E e F, então:
- AD = AF
- BD = BE
- CE = CF
Essas igualdades permitem montar expressões para calcular perímetros e áreas com facilidade.
💡 3. Exemplo prático
Um ponto P está fora de uma circunferência. As tangentes PA e PB medem x + 2 e 3x − 4.
Sabendo que PA = PB, temos:
x + 2 = 3x − 4
2 + 4 = 3x − x
x = 3
Logo, PA = PB = 5 cm.
🧠 4. Integração com o Teorema de Pitágoras e semelhança de triângulos
Em muitas questões, o ponto externo P está ligado ao centro O da circunferência, formando triângulos retângulos (pois o raio é perpendicular à tangente).
➡️ Assim, é comum aplicar o Teorema de Pitágoras:
OP² = OA² + PA²
ou usar semelhança de triângulos para relacionar partes proporcionais e encontrar medidas faltantes.
📚 Resumindo:
- Use PA = PB para criar equações simples.
- Use Pitágoras quando houver o centro da circunferência.
- Use semelhança de triângulos em problemas com várias tangentes.
- Em triângulos circunscritos, as três igualdades das tangentes permitem montar equações elegantes de perímetro e área.
✅ Exemplo 1 — (fácil) Cálculo direto com PA = PB
Enunciado. De um ponto externo P saem duas tangentes ao círculo, tocando-o em A e B. Sabendo que
PA = x + 2 e PB = 3x − 4, determine x e o valor de PA e PB.
Solução. Como as tangentes a partir de um mesmo ponto são iguais,
PA = PB ⇒ x + 2 = 3x − 4 ⇒ 6 = 2x ⇒ x = 3.
Logo, PA = PB = x + 2 = 5 (na mesma unidade do enunciado).
Resposta. x = 3 e PA = PB = 5.
🧭 Exemplo 2 — (médio) Triângulo circunscrito e segmentos iguais
Enunciado. O triângulo ABC é circunscrito a uma circunferência (incírculo). Sabendo que
AB = 13, BC = 14 e CA = 15, encontre os comprimentos dos segmentos de tangência a partir de cada vértice.
Ideia-chave. Em triângulo circunscrito, dos mesmos vértices saem tangentes de comprimentos iguais:
- De A: segmentos sobre AB e AC valem s − a
- De B: segmentos sobre AB e BC valem s − b
- De C: segmentos sobre AC e BC valem s − c
Aqui: a = BC = 14, b = CA = 15, c = AB = 13 e o semiperímetro é
s = (13 + 14 + 15) ÷ 2 = 21.
Portanto:
- De A: s − a = 21 − 14 = 7 (então os trechos em AB e AC que partem de A medem 7).
- De B: s − b = 21 − 15 = 6.
- De C: s − c = 21 − 13 = 8.
Checagem rápida:
AB = 7 + 6 = 13, AC = 7 + 8 = 15, BC = 6 + 8 = 14 ✅
Bônus (área). A área do triângulo é A = r × s. Se precisar do raio r, pode obtê-lo com Heron ou reconhecendo o triângulo 13-14-15 (r = 4). Assim, A = 4 × 21 = 84.
🔬 Exemplo 3 — (difícil) PA com Pitágoras e ângulo entre tangentes
Enunciado. Um ponto P está a OP = 13 do centro O de um círculo de raio r = 5.
a) Calcule PA.
b) Calcule o ângulo ∠APB entre as tangentes.
Passo 1. Comprimento PA. No triângulo retângulo OAP (raio ⟂ tangente),
OP² = OA² + PA² ⇒ 13² = 5² + PA² ⇒ 169 = 25 + PA² ⇒ PA = 12.
Passo 2. Ângulo entre as tangentes.
No triângulo OAP, cos θ = OA ÷ OP = 5 ÷ 13 ⇒ θ ≈ arccos(5 ÷ 13) ≈ 67,38°.
O ângulo central ∠AOB = 2θ e o ângulo entre as tangentes é
∠APB = 180° − 2θ ≈ 180° − 134,76° = 45,24°.
Resposta. PA = 12 e ∠APB ≈ 45,24°.
⚠️ Erros que mais reprovam
- Confundir tangente com secante (tangente toca em 1 ponto; secante corta em 2).
- Esquecer PA = PB e tentar somá-los em vez de igualá-los.
- Ignorar o raio ⟂ tangente e perder o triângulo retângulo para aplicar Pitágoras.
- Misturar segmentos do triângulo circunscrito (no exemplo do incírculo, use sempre s − a, s − b, s − c).
- Tratar ângulo entre tangentes como ângulo central (lembre: ∠APB = 180° − ∠AOB).
5️⃣ Por que esse teorema cai tanto em concursos?
🎯 Alta frequência nas provas militares (EEAR, ESA, EsPCEx e Colégio Naval)
O Teorema dos Segmentos Tangentes aparece quase todos os anos em provas dessas escolas porque ele combina interpretação geométrica, raciocínio lógico e aplicação direta de fórmulas — exatamente o que as bancas buscam avaliar.
📚 Estatísticas de incidência aproximada:
- EEAR: 2 a 3 questões de geometria por prova, e o teorema já apareceu em 4 dos últimos 6 anos.
- ESA: cai frequentemente em figuras com circunferências tangentes a triângulos.
- EsPCEx: costuma aparecer de forma disfarçada, dentro de problemas de áreas e semelhanças.
- Colégio Naval: cobra em contextos de construções geométricas e relação entre ângulos e tangentes.
🧭 Por que as bancas gostam desse tipo de problema?
✔️ É visual e intuitivo, fácil de representar com figuras simples, mas exige interpretação geométrica precisa.
✔️ Testa conceitos fundamentais (tangência, igualdade de segmentos, triângulos retângulos, Pitágoras).
✔️ Permite criar armadilhas sutis — confusões entre tangente e secante, ou entre ângulo central e ângulo formado pelas tangentes.
✔️ Pode ser resolvido rapidamente com um bom olhar geométrico, o que diferencia os candidatos mais preparados.
⚙️ Interpretação + aplicação = perfil ideal de candidato militar
As provas militares valorizam a disciplina de raciocínio lógico. O aluno precisa:
- Identificar o ponto externo e os pontos de tangência;
- Relacionar os segmentos iguais;
- Montar equações simples;
- Aplicar Pitágoras ou propriedades de triângulos.
👉 Em poucos passos, o avaliador sabe quem entende geometria de verdade e quem apenas decora fórmulas.
📘 Comentário de questão real – ESA 2022
“De um ponto P exterior a uma circunferência de raio 4 cm, traçam-se duas tangentes PA e PB, e a distância do ponto P ao centro da circunferência é 10 cm. Determine o comprimento de PA.”
Resolução:
O raio é perpendicular à tangente ⇒ triângulo OAP é retângulo.
OP² = OA² + PA²
10² = 4² + PA²
100 = 16 + PA²
PA² = 84
PA = √84 ≈ 9,17 cm
✅ Comentário:
Questão clássica, de resolução direta, mas que exige atenção ao conceito de tangência. Muitos candidatos erram ao usar fórmula de secante ou tentar somar as medidas.
🔥 Resumo prático:
- O teorema cai muito porque é curto, visual e conceitual.
- Serve como filtro para quem domina raciocínio geométrico rápido.
- É porta de entrada para questões mais elaboradas de círculo, semelhança e áreas.
🟢 6️⃣ Dicas para memorizar o Teorema dos Segmentos Tangentes
🧩 1️⃣ Mapa mental visual
Monte uma imagem mental (ou desenhe) com esta sequência:
👉 Ponto externo (P) →
👉 Duas tangentes (PA e PB) →
👉 Tocam a circunferência →
👉 Pontos de tangência (A e B) →
👉 Segmentos iguais (PA = PB)
💭 Imagine o ponto P como “um observador fora do círculo” tocando a borda em dois lugares distintos.
Essas duas linhas são “gêmeas” — partem do mesmo ponto e chegam ao círculo na mesma distância.
🧠 2️⃣ Frase mnemônica para fixar
📢 “Tangentes do mesmo ponto são como irmãos gêmeos: medem igual!”
Essa frase resume o conceito inteiro de forma divertida e fácil de lembrar. 😄
✏️ 3️⃣ Pratique com desenhos rápidos
Treine sempre com pequenos esboços no caderno:
- Um círculo
- Um ponto fora dele
- Duas tangentes tocando a borda
Depois, marque: PA = PB, e desenhe os raios perpendiculares aos pontos de tangência (OA ⟂ PA e OB ⟂ PB).
Esse hábito ajuda o cérebro a associar visual + lógica + fórmula.
📚 4️⃣ Use flashcards inteligentes
Monte flashcards (cartões de estudo) com perguntas e imagens:
🟦 Frente: “De um ponto P, traçam-se duas tangentes PA e PB. Qual a relação entre elas?”
🟩 Verso: “São iguais! PA = PB (Teorema dos Segmentos Tangentes).”
Também dá para criar versões numéricas:
“Se PA = x + 3 e PB = 2x − 1, qual o valor de x?”
👉 Esse tipo de treino rápido é excelente para fixar o padrão das questões de prova.
💡 5️⃣ Dica bônus – Associação com outros teoremas
Relacione este teorema ao Teorema da Potência de um Ponto, que diz:
Para tangente e secante: PT² = PE × PF
Assim, você entende como os segmentos tangentes são uma forma especial dessa relação — quando a secante se transforma em duas tangentes iguais.
✨ Resumo da memorização:
- Visualize → desenhe → repita.
- Use a frase “irmãos gêmeos”.
- Pratique com flashcards.
- Compare com o Teorema da Potência.
- E lembre sempre: Ponto externo → tangentes iguais → Pitágoras à vista! 📐🔥
🟢 7️⃣ Como esse teorema se conecta com outros conteúdos do edital
🔗 1️⃣ Relação com o Teorema de Pitágoras
O Teorema dos Segmentos Tangentes é quase sempre acompanhado do Pitágoras, porque o raio é perpendicular à tangente.
Assim, forma-se naturalmente um triângulo retângulo entre:
- o raio (r),
- o segmento tangente (PA),
- e a distância do ponto externo ao centro (OP).
📐 Exemplo típico:
Se OP = 13 e r = 5, então
OP² = OA² + PA² → 13² = 5² + PA² → PA = 12.
➡️ Isso já apareceu em EEAR 2021 e ESA 2022.
📏 2️⃣ Conexão com triângulos retângulos
Os triângulos formados pela tangente e o raio são retângulos e, em muitos problemas, aparecem dois triângulos simétricos (OAP e OBP).
Esses triângulos podem ser:
- congruentes, pois possuem lados iguais (r, r e PA = PB);
- semelhantes, quando o ponto externo é ligado ao centro, formando figuras proporcionais.
📚 Questões assim testam o reconhecimento de ângulos retos e simetria — tema recorrente em EsPCEx e Colégio Naval.
⚖️ 3️⃣ Ligação com Razão e Proporção
Quando o problema envolve prolongamentos de tangentes ou secantes, as bancas misturam o Teorema dos Segmentos Tangentes com relações proporcionais:
PA = PB → pode levar a razões como PA / PB = 1 ou proporções entre triângulos semelhantes.
Além disso, o Teorema da Potência de um Ponto (PT² = PE × PF) é uma extensão direta, muito cobrada em provas da EEAR.
📐 4️⃣ Relação com áreas de figuras planas
Tangentes aparecem em triângulos circunscritos e quadriláteros tangenciais, onde os lados opostos somam o mesmo valor.
📌 Fórmula útil:
Para um triângulo circunscrito, se o semiperímetro é s, então as tangentes a partir de cada vértice valem s − a, s − b, s − c.
Com isso, é possível calcular áreas e perímetros de forma rápida.
➡️ Essa integração caiu na ESA 2023, em uma questão que pedia o raio da circunferência inscrita a partir dos lados do triângulo.
🧠 5️⃣ Questões interdisciplinares e raciocínio lógico
As bancas adoram combinar teoremas para avaliar se o candidato consegue enxergar conexões:
🔸 Pitágoras + Tangentes → medir segmentos iguais e ângulos;
🔸 Semelhança + Razões → comparar triângulos formados;
🔸 Áreas + Circunferências → deduzir raio ou lado faltante.
📘 Exemplo (EsPCEx 2020):
“De um ponto fora de uma circunferência de raio 6 cm, traçam-se duas tangentes formando entre si um ângulo de 60°. Calcule a distância do ponto ao centro.”
Solução: Triângulo isósceles com dois lados iguais (OP e OP) e base relacionada ao ângulo formado.
Usa-se Pitágoras e trigonometria:
OP = r / sen(θ/2) = 6 / sen(30°) = 12 cm.
💡 Resumo prático das conexões:
| Conteúdo | Ligação com o Teorema dos Segmentos Tangentes |
|---|---|
| Pitágoras | O raio é ⟂ à tangente → triângulo retângulo |
| Triângulos | Formação de triângulos congruentes ou semelhantes |
| Razão e Proporção | Igualdade dos segmentos → proporções geométricas |
| Áreas Planas | Triângulos e quadriláteros circunscritos |
🚀 Conclusão:
O Teorema dos Segmentos Tangentes é um ponto de conexão entre vários conteúdos do edital.
Ele transforma uma figura simples em um laboratório de raciocínio geométrico — exatamente o tipo de questão que separa quem entende a lógica por trás da geometria de quem apenas decora fórmulas.
🧠 SABE O QUE É UM APÓTEMA?
Você já ouviu essa palavra em sala de aula e pensou:
“Isso vai cair na prova…” 👀
Pois saiba que apótema é um dos conceitos mais importantes da geometria plana, especialmente para quem estuda para ESA, EEAR, EPCAR, CFN e concursos militares.
E hoje você vai entender de forma clara, visual e aplicável.
📌 1️⃣ O QUE É APÓTEMA?
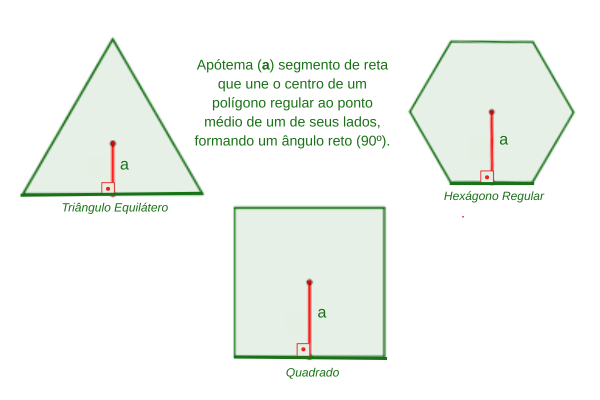
A apótema é o segmento que liga o centro de um polígono regular até o ponto médio de um de seus lados, formando um ângulo de 90°.
Em termos simples:
✔ É a distância do centro até o lado.
✔ É sempre perpendicular ao lado.
✔ Só existe formalmente em polígonos regulares.
📐 2️⃣ POR QUE O TRIÂNGULO EQUILÁTERO É ESPECIAL?
Vejam todos os Pontos Notáveis existentes :
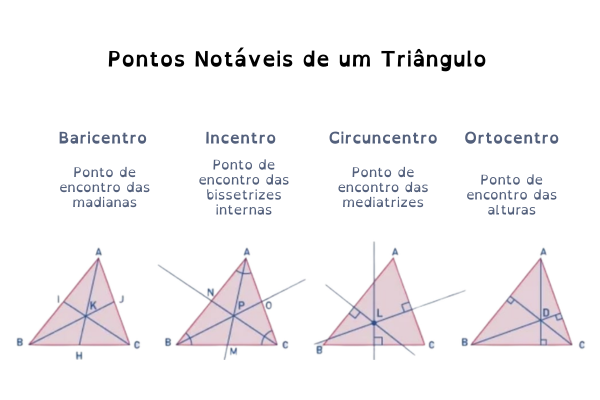
Baricentro (K) – é o ponto de encontro das três medianas de um triângulo, representando seu centro de gravidade ou centro de massa. Ele divide cada mediana na proporção de 2:1 (a parte do vértice é o dobro da parte do ponto médio) e está sempre no interior do triângulo.
- Incentro (P) – é o ponto notável de um triângulo formado pela intersecção das suas três bissetrizes internas, representando o centro da circunferência inscrita (tangente aos três lados)
- Circuncentro (L) – é o ponto de encontro das mediatrizes (retas perpendiculares nos pontos médios) dos lados de um triângulo, sendo o centro da circunferência que circunscreve o polígono e equidistante dos seus três vértices.
- Ortocentro – é o ponto de interseção das três alturas de um triângulo, onde cada altura é o segmento perpendicular que liga um vértice ao lado oposto.
Isso faz com que o estudo da apótema fique muito mais elegante, porque em um triângulo retângulo acontece algo incrível:
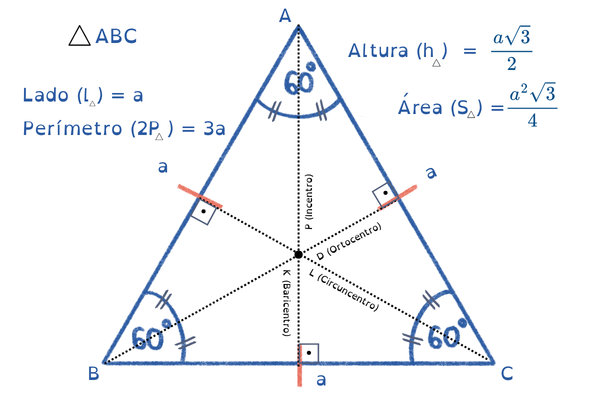
- O ponto de encontro da mediana, altura, bissetriz e mediatriz, coincidem no mesmo ponto.
🔥 3️⃣ RELAÇÃO ENTRE ALTURA E APÓTEMA
Altura do triângulo equilátero:
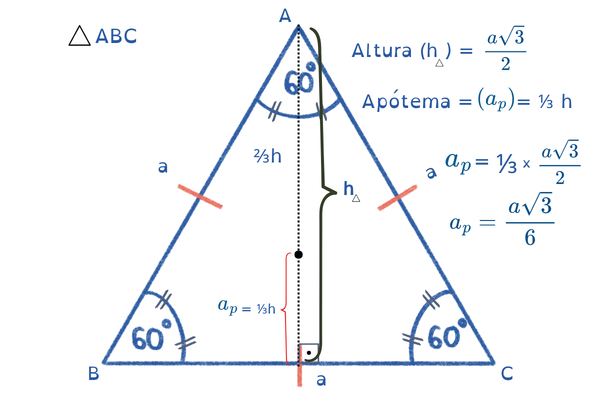
👉 A apótema é 1/3 da altura.
Essa é uma das pegadinhas favoritas de concurso.
🚀 APLICAÇÃO 1
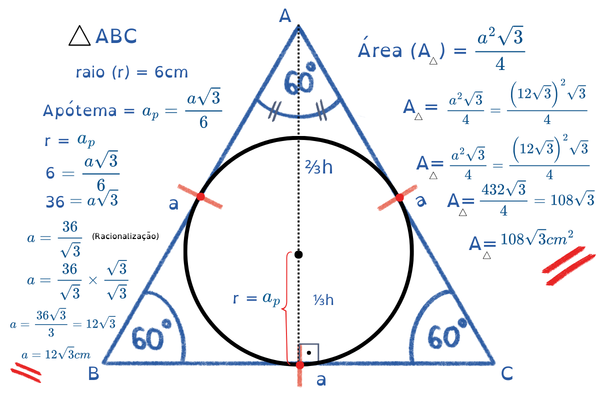
Circunferência INSCRITA no triângulo equilátero, encontre o lado (a) e a área (A) do triângulo equilátero.
Dado: r = 6 cm

🚀 APLICAÇÃO 2
Circunferência CIRCUNSCRITA ao triângulo equilátero, encontre o lado (a) e área (A)
Agora vamos inverter o raciocínio.
Raio da circunferência circunscrita (r): r = 8 cm
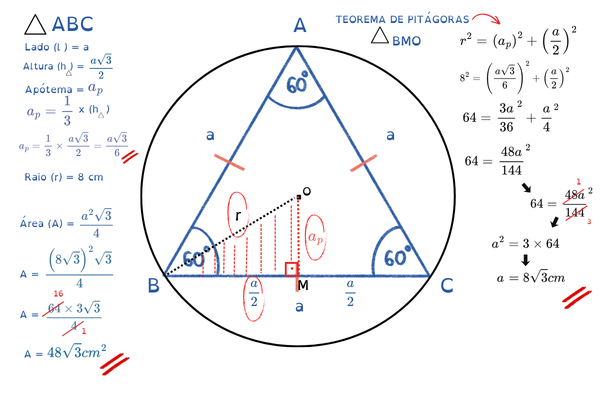
⚔️ DIFERENÇA IMPORTANTE PARA CONCURSOS
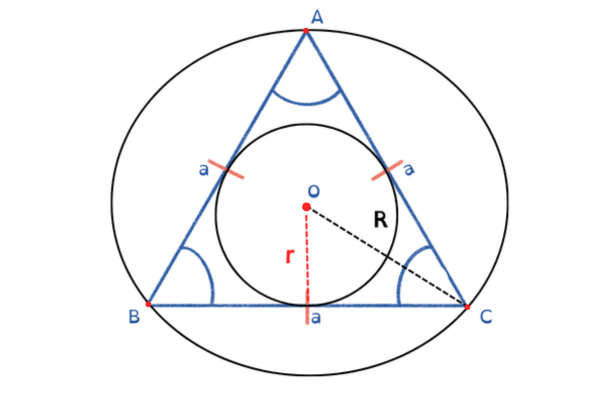
👉 A circunferência inscrita fica dentro do triângulo, tangenciando os três lados.
⚔️ DIFERENÇA QUE CAI EM PROVA MILITAR
🎯 Triângulo Equilátero
Existe uma diferença MUITO importante entre:
🔵 Circunferência Inscrita
🔴 Circunferência Circunscrita
E a banca AMA confundir isso.
🔵 1️⃣ CIRCUNFERÊNCIA INSCRITA
👉 Fica dentro do triângulo
👉 Toca os três lados
📌 Fórmula do raio (r):
r = (a√3) / 6
Onde:
a = lado do triângulo
💡 Relação com a altura
Altura do triângulo equilátero:
h = (a√3) / 2
Observe:
r = h / 3
⚠️ A apótema é 1/3 da altura.
Essa é pegadinha clássica.
🔴 2️⃣ CIRCUNFERÊNCIA CIRCUNSCRITA
👉 Fica por fora do triângulo
👉 Passa pelos três vértices
📌 Fórmula do raio (R):
R = (a√3) / 3
🔥 3️⃣ RELAÇÃO QUE DESPENCA EM PROVA
Temos:
r = (a√3) / 6 => r = R/2 => R = 2r
R = (a√3) / 3
🚨 CONCLUSÃO IMPORTANTE
🔴 O raio da circunferência circunscrita é o DOBRO do raio da inscrita.
Se a banca der:
• o valor de r → você multiplica por 2 para achar R
• o valor de R → divide por 2 para achar r
📚 QUER TREINAR AGORA?
Preparamos uma lista especial com questões nível ESA, EEAR e CFN envolvendo:
✔ Apótema
✔ Circunferência inscrita
✔ Circunferência circunscrita
✔ Área
✔ Relação entre alturas
👉 Vá agora na categoria “Baixe Aki” do blog e faça o download gratuito.
Treinar é o que transforma teoria em aprovação.
💡 CONCLUSÃO
Apótema não é apenas um segmento geométrico.
É uma ferramenta estratégica para:
- Resolver áreas rapidamente
- Evitar pegadinhas
- Ganhar tempo de prova
- Resolver questões de nível militar
Se esse conteúdo te ajudou, compartilhe com alguém que está estudando para concurso.
E continue acompanhando o blog.
Porque aqui, você aprende para passar.
📘 Binômio de Newton do Básico ao Avançado

🔹 1. Por que o Binômio de Newton parece tão difícil?
O Binômio de Newton está entre aqueles assuntos que, à primeira vista, parecem desafiadores. 🤯
Quando o estudante se depara com expressões como (a + b)¹⁰, é comum imaginar que isso envolverá cálculos gigantescos, repetitivos e complicados. Essa primeira impressão cria um bloqueio psicológico imediato — mesmo antes de tentar entender a lógica do conteúdo.
Mas a verdade é simples:
👉 o binômio não é difícil; ele só parece difícil.
A estrutura é organizada, padronizada e previsível. Quando você entende o padrão, tudo se torna mais claro e até intuitivo.
🤯 Sensação de complexidade
A aparência assusta.
Quando vemos (a + b)⁸, (x − 2)⁶ ou (3a + b)⁵, o cérebro automaticamente pensa em multiplicações intermináveis.
Isso cria a falsa ideia de que estamos diante de algo avançado demais.
Mas o Binômio de Newton existe justamente para evitar essa multiplicação enorme. Ele oferece um método direto e elegante para obter o resultado sem sofrimento.
🔀 Mistura de conteúdos
O principal motivo da dificuldade é que o binômio une três conteúdos diferentes da matemática. Quem não domina um deles acaba sentindo o impacto.
• Potenciação
É preciso entender como os expoentes se distribuem:
- o primeiro termo começa com expoente máximo (ex.: a¹⁰) e vai diminuindo;
- o segundo termo começa com expoente 0 (ex.: b⁰) e vai aumentando.
• Polinômios
O aluno precisa saber:
- organizar termos,
- identificar coeficientes,
- combinar expressões de forma limpa.
• Combinatória
Os coeficientes do binômio vêm das combinações:
- C(n, k) = coeficiente do termo k
E aparecem automaticamente no Triângulo de Pascal.
Essa combinação tripla é o que mais confunde quem está começando.
🎯 Por que cai tanto em concursos?
O Binômio de Newton é um dos assuntos favoritos das bancas porque ele mede várias habilidades ao mesmo tempo:
✔ Testa raciocínio lógico
O candidato precisa identificar padrões, simetrias e progressões.
✔ Explora padrões numéricos
Coeficientes, expoentes, termos e combinações surgem em perfeita organização.
✔ Avalia domínio algébrico
Manipular expressões como (a + b)⁵ exige atenção às regras da álgebra.
Por isso é tão cobrado em:
- EEAR
- EsPCEx
- EPCAR
- ESA
- Colégio Naval
- Petrobras
- Transpetro
- Processos seletivos técnicos e militares
Dominar esse conteúdo não só facilita a prova — como também aumenta muito a confiança do aluno em álgebra.
🔹 2. Pré-requisitos essenciais antes de estudar o Binômio de Newton
Para dominar o Binômio de Newton, o aluno precisa antes construir uma base sólida. O binômio reúne conceitos de potenciação, polinômios e combinatória — e quando um desses pilares falta, o conteúdo parece mais difícil do que realmente é.
Com os pré-requisitos em dia, o assunto se torna leve, lógico e até prazeroso de estudar. ✨
🔢 1. Potenciação e propriedades
A expansão de um binômio segue um padrão claro de expoentes.
Por isso, é fundamental dominar operações como:
- aᵐ × aⁿ = aᵐ⁺ⁿ
- (aᵐ)ⁿ = aᵐⁿ
- a⁻ⁿ = 1 / aⁿ
- sinais em potências:
- (−a)ⁿ → positivo se n for par
- (−a)ⁿ → negativo se n for ímpar
Por que isso importa?
Na expansão de (a + b)ⁿ, os expoentes seguem uma lógica:
- o primeiro termo começa com aⁿ e vai até a⁰,
- o segundo começa com b⁰ e vai até bⁿ.
Se o aluno domina expoentes, a expansão vira apenas um padrão, não um mistério.
🧩 2. Produtos notáveis
Antes de expandir (a + b)¹⁰, o aluno precisa compreender o que acontece com expoentes menores.
Exemplos essenciais:
- (a + b)² = a² + 2ab + b²
- (a + b)³ = a³ + 3a²b + 3ab² + b³
Essas fórmulas ajudam a visualizar:
- como os expoentes se distribuem,
- como surgem os coeficientes,
- como o binômio cresce de forma previsível.
São mini versões do Binômio de Newton.
❗ 3. Fatorial: a base dos coeficientes
Os coeficientes do binômio são obtidos por combinações, que usam fatorial.
Por isso, é fundamental entender:
- 4! = 4 × 3 × 2 × 1 = 24
- 0! = 1 (regra essencial)
- relação recursiva:
n! = n × (n−1)!
Sem dominar fatorial, o cálculo de combinações fica confuso e cria um bloqueio desnecessário.
🎲 4. Combinação simples C(n, k)
Os coeficientes da expansão vêm diretamente de:
C(n, k) = n! ÷ (k! × (n−k)!)
Essa combinação gera cada número da expansão de (a + b)ⁿ.
Exemplos:
- C(2, 1) = 2 → aparece em (a + b)²
- C(3, 2) = 3 → aparece em (a + b)³
- C(5, 2) = 10 → aparece em (a + b)⁵
Esses números são os coeficientes — exatamente os mesmos que aparecem no Triângulo de Pascal.
✔ Essencial para avançar
Quando você domina:
- expoentes,
- produtos notáveis,
- fatorial,
- e combinações,
o Binômio de Newton deixa de ser um desafio e se transforma num conteúdo organizado, lógico e até elegante.
🔹 4. Triângulo de Pascal: origem dos coeficientes
Para entender o Binômio de Newton de verdade, o aluno precisa conhecer a estrutura que gera todos os coeficientes da expansão: o Triângulo de Pascal.
Ele é simples, elegante e incrivelmente poderoso. Com ele, é possível expandir (a + b)ⁿ sem fórmulas, sem decorar nada e sem fazer cálculos longos. 🔺✨
📐 Como construir o Triângulo de Pascal
A construção é intuitiva:
- Comece com o número 1 no topo.
- Cada nova linha começa e termina com 1.
- Cada número do meio é a soma dos dois números acima.
📌Visualmente (representação simples):
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
🔗 Como o Triângulo se conecta ao Binômio
Cada linha do Triângulo corresponde exatamente aos coeficientes da expansão de um binômio.
Exemplos:
- Linha 2 → coeficientes de (a + b)²→ 1, 2, 1
- Linha 3 → coeficientes de (a + b)³→ 1, 3, 3, 1
- Linha 5 → coeficientes de (a + b)⁵→ 1, 5, 10, 10, 5, 1
Ou seja:
👉 Basta olhar a linha correspondente ao expoente para saber todos os coeficientes da expansão.
Isso evita cálculos, evita erros e acelera a resolução de questões de concurso.
🧠 O padrão matemático por trás do triângulo
Cada número do Triângulo de Pascal representa uma combinação simples:
C(n, k)
Por exemplo, na linha 5:
- C(5, 0) = 1
- C(5, 1) = 5
- C(5, 2) = 10
- C(5, 3) = 10
- C(5, 4) = 5
- C(5, 5) = 1
Isso significa que o triângulo é uma forma geométrica de visualizar as combinações que aparecem na fórmula do Binômio de Newton.
✨ É matemática visual — exatamente o tipo de ferramenta que transforma dificuldade em clareza.
⚡ Por que o Triângulo de Pascal facilita tanto?
- Ele entrega todos os coeficientes prontos.
- Permite expandir binômios rapidamente.
- Evita cálculos com fatorial quando não são necessários.
- Mostra simetria e repetição, ajudando na memorização.
- Ajuda a entender a estrutura da expansão antes mesmo de usar a fórmula geral.
Para muitos alunos, o Triângulo de Pascal é o ponto em que o Binômio de Newton deixa de ser “assustador” e passa a fazer sentido.
🔹 5. A fórmula geral do Binômio de Newton (com exemplos simples)
Depois de entender os padrões e o Triângulo de Pascal, é hora de ver como o Binômio de Newton funciona na prática. A fórmula geral é poderosa porque permite expandir qualquer expressão do tipo (a + b)ⁿ sem multiplicações longas.
Ela organiza tudo: coeficientes, expoentes e termos — sempre seguindo o mesmo padrão. ✨
📘 A fórmula geral
A expansão de (a + b)ⁿ é dada por:
(a + b)ⁿ = C(n, 0)aⁿb⁰ + C(n, 1)aⁿ⁻¹b¹ + C(n, 2)aⁿ⁻²b² + … + C(n, n)a⁰bⁿ
Em outras palavras:
Cada termo é formado por:
✔ um coeficiente C(n, k)
✔ uma potência decrescente de a
✔ uma potência crescente de b
✨ Exemplos Simples e Objetivos
🔹 EXEMPLO 1: Expandir (a + b)²
Passo 1 — Coeficientes da linha 2:
1, 2, 1
Passo 2 — Expoentes:
- a², a¹, a⁰
- b⁰, b¹, b²
Passo 3 — Montagem:
(a + b)² = a² + 2ab + b²
Simples, direto e previsível.
🔹 EXEMPLO 2: Expandir (a + b)³
Coeficientes (linha 3):
1, 3, 3, 1
Expoentes:
- a³, a², a¹, a⁰
- b⁰, b¹, b², b³
Montagem:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Novamente, o padrão se repete perfeitamente.
🔹 EXEMPLO 3: Expandir (x + 1)³
Coeficientes:
1, 3, 3, 1
Montando os termos:
- 1 · x³ · 1⁰ = x³
- 3 · x² · 1¹ = 3x²
- 3 · x¹ · 1² = 3x
- 1 · x⁰ · 1³ = 1
Resultado:
(x + 1)³ = x³ + 3x² + 3x + 1
Esse é um dos binômios mais usados em provas e aparece com frequência em manipulações algébricas.
🔹 EXEMPLO 4: Expandir (2a + b)²
Coeficientes:
1, 2, 1
Termos:
- 1 · (2a)² · b⁰ = 4a²
- 2 · (2a)¹ · b¹ = 4ab
- 1 · (2a)⁰ · b² = b²
Resultado:
(2a + b)² = 4a² + 4ab + b²
Aqui vemos como a fórmula lida facilmente com coeficientes dentro do binômio.
🔹 EXEMPLO 5: Primeiro termo de (x − 3)⁵
Usando o termo geral:
T₁ = C(5, 0) · x⁵ · (−3)⁰ = x⁵
E o segundo:
T₂ = C(5, 1) · x⁴ · (−3)¹
T₂ = 5x⁴(−3) = −15x⁴
Ou seja, conseguimos extrair apenas os termos desejados, sem precisar expandir tudo.
🔍 Resumo do que você precisa enxergar
- Os expoentes seguem um padrão fixo
- Os coeficientes vêm sempre do Triângulo de Pascal
- O termo geral permite pegar qualquer termo sem expandir tudo
- O binômio é muito mais organizado do que parece
Quando você entende isso, (a + b)ⁿ deixa de ser temido e passa a ser apenas mais uma ferramenta matemática — muito útil em concursos.
🔹 6. Conexão entre C(n, k) e os coeficientes do binômio
Os coeficientes que aparecem na expansão de (a + b)ⁿ não surgem por acaso. Eles têm uma origem combinatória e seguem uma lógica perfeita.
Cada número que aparece na expansão é, na verdade, uma combinação simples — aquelas estudadas em análise combinatória.
E entender essa conexão é fundamental para dominar o Binômio de Newton.
É aqui que a matemática deixa de ser apenas regras e passa a revelar seus padrões internos. ✨
🎲 C(n, k): a fórmula que gera todos os coeficientes
A combinação simples é dada por:
C(n, k) = n! ÷ (k! × (n − k)!)
Essa expressão calcula quantas maneiras diferentes podemos escolher k elementos dentro de um conjunto com n elementos.
Mas o que isso tem a ver com o binômio?
👉 Tudo.
Porque cada termo da expansão de (a + b)ⁿ aparece exatamente C(n, k) vezes quando multiplicamos tudo sem organização.
A fórmula do binômio apenas transforma isso em método organizado.
✔ Como a combinação aparece na prática
Veja a expansão de (a + b)³:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Os coeficientes 1, 3, 3, 1 vêm diretamente das combinações:
- C(3, 0) = 1
- C(3, 1) = 3
- C(3, 2) = 3
- C(3, 3) = 1
A soma dos expoentes de cada termo sempre dá 3, e o coeficiente indica quantas vezes cada termo aparece nas multiplicações.
✔ Outro exemplo: coeficientes de (a + b)⁵
Linha 5 do Triângulo de Pascal:
1, 5, 10, 10, 5, 1
Agora olhando pelas combinações:
- C(5, 0) = 1
- C(5, 1) = 5
- C(5, 2) = 10
- C(5, 3) = 10
- C(5, 4) = 5
- C(5, 5) = 1
Ou seja, o Triângulo de Pascal nada mais é do que uma forma visual de representar C(n, k).
🔍 Por que essa conexão é tão importante?
- Traz lógica ao binômio
O aluno começa a entender por que os coeficientes são aqueles — não apenas decorá-los. - Facilita o cálculo de termos específicos
Muitas questões de concurso pedem apenas “o terceiro termo”, “o termo independente”, etc.
Com C(n, k), você resolve isso em segundos. - Evita erros
A fórmula de combinação é sempre segura.
Mesmo que você não monte o triângulo, o cálculo será correto. - Conecta o binômio à combinatória e probabilidade
O conteúdo fica mais rico e interdisciplinar.
✨ Enxergue assim:
C(n, k) = o coeficiente que multiplica o termo aⁿ⁻ᵏ · bᵏ na expansão.
Simples, direto e universal.
Essa relação vale para qualquer valor de n, seja pequeno ou enorme.
🔹 6. Conexão entre C(n, k) e os coeficientes do binômio
Os coeficientes que aparecem na expansão de (a + b)ⁿ não surgem por acaso. Eles têm uma origem combinatória e seguem uma lógica perfeita.
Cada número que aparece na expansão é, na verdade, uma combinação simples — aquelas estudadas em análise combinatória.
E entender essa conexão é fundamental para dominar o Binômio de Newton.
É aqui que a matemática deixa de ser apenas regras e passa a revelar seus padrões internos. ✨
🎲 C(n, k): a fórmula que gera todos os coeficientes
A combinação simples é dada por:
C(n, k) = n! ÷ (k! × (n − k)!)
Essa expressão calcula quantas maneiras diferentes podemos escolher k elementos dentro de um conjunto com n elementos.
Mas o que isso tem a ver com o binômio?
👉 Tudo.
Porque cada termo da expansão de (a + b)ⁿ aparece exatamente C(n, k) vezes quando multiplicamos tudo sem organização.
A fórmula do binômio apenas transforma isso em método organizado.
✔ Como a combinação aparece na prática
Veja a expansão de (a + b)³:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Os coeficientes 1, 3, 3, 1 vêm diretamente das combinações:
- C(3, 0) = 1
- C(3, 1) = 3
- C(3, 2) = 3
- C(3, 3) = 1
A soma dos expoentes de cada termo sempre dá 3, e o coeficiente indica quantas vezes cada termo aparece nas multiplicações.
✔ Outro exemplo: coeficientes de (a + b)⁵
Linha 5 do Triângulo de Pascal:
1, 5, 10, 10, 5, 1
Agora olhando pelas combinações:
- C(5, 0) = 1
- C(5, 1) = 5
- C(5, 2) = 10
- C(5, 3) = 10
- C(5, 4) = 5
- C(5, 5) = 1
Ou seja, o Triângulo de Pascal nada mais é do que uma forma visual de representar C(n, k).
🔍 Por que essa conexão é tão importante?
- Traz lógica ao binômio
O aluno começa a entender por que os coeficientes são aqueles — não apenas decorá-los. - Facilita o cálculo de termos específicos
Muitas questões de concurso pedem apenas “o terceiro termo”, “o termo independente”, etc.
Com C(n, k), você resolve isso em segundos. - Evita erros
A fórmula de combinação é sempre segura.
Mesmo que você não monte o triângulo, o cálculo será correto. - Conecta o binômio à combinatória e probabilidade
O conteúdo fica mais rico e interdisciplinar.
✨ Enxergue assim:
C(n, k) = o coeficiente que multiplica o termo aⁿ⁻ᵏ · bᵏ na expansão.
Simples, direto e universal.
Essa relação vale para qualquer valor de n, seja pequeno ou enorme.
🔹 7. Exemplos básicos, intermediários e avançados
Agora que você já entende os padrões, os coeficientes e a relação com C(n, k), é hora de ver o Binômio de Newton funcionando na prática.
Vamos dividir os exemplos em 3 níveis de dificuldade — assim o aluno consegue evoluir de forma natural e confiante.
⭐ EXEMPLOS BÁSICOS
Esses exemplos reforçam a estrutura do binômio e ajudam a fixar os padrões iniciais.
✔ 1. Expansão de (a + b)²
Coeficientes: 1, 2, 1
Expoentes organizados:
- a², a¹, a⁰
- b⁰, b¹, b²
Resultado:
(a + b)² = a² + 2ab + b²
✔ 2. Expansão de (x − 1)²
Coeficientes: 1, 2, 1
Atenção ao sinal:
- x²
- −2x
- 1
Resultado:
(x − 1)² = x² − 2x + 1
⭐⭐ EXEMPLOS INTERMEDIÁRIOS
Agora com expoentes maiores e expressões mais ricas.
✔ 3. Expandir (a + b)³
Coeficientes: 1, 3, 3, 1
(a + b)³ = a³ + 3a²b + 3ab² + b³
✔ 4. Expandir (x + 2)³
Coeficientes: 1, 3, 3, 1
Termos:
- x³
- 3x²·2 = 6x²
- 3x·2² = 12x
- 2³ = 8
Resultado:
(x + 2)³ = x³ + 6x² + 12x + 8
✔ 5. Expandir (2a + b)³
Coeficientes: 1, 3, 3, 1
Termos:
- (2a)³ = 8a³
- 3·(2a)²·b = 12a²b
- 3·(2a)·b² = 6ab²
- b³
Resultado:
(2a + b)³ = 8a³ + 12a²b + 6ab² + b³
⭐⭐⭐ EXEMPLOS AVANÇADOS
Esses exemplos aparecem com frequência em concursos militares e bancas técnicas.
✔ 6. Encontrar o terceiro termo da expansão de (x − 3)⁵
Usaremos o termo geral:
Tₖ₊₁ = C(n, k) · aⁿ⁻ᵏ · bᵏ
Para o 3º termo, k = 2.
- n = 5
- C(5, 2) = 10
- a = x
- b = −3
Aplicando:
T₃ = 10 · x³ · (−3)²
T₃ = 10 · x³ · 9
T₃ = 90x³
Resposta:
O 3º termo é 90x³.
✔ 7. Encontrar o termo independente em (2x − 1)⁴
Termo independente = termo que NÃO tem x.
Usamos o termo geral:
Tₖ₊₁ = C(4, k) · (2x)⁴⁻ᵏ · (−1)ᵏ
Queremos que o expoente de x seja zero:
(2x)⁴⁻ᵏ → x⁴⁻ᵏ
Então:
4 − k = 0
k = 4
Agora substituímos:
T₅ = C(4, 4) · (2x)⁰ · (−1)⁴
T₅ = 1 · 1 · 1 = 1
Resultado:
O termo independente é 1.
✔ 8. Coeficiente do termo em x³ em (1 + x)⁷
Queremos o termo com x³ → então k = 3.
Coeficiente = C(7, 3)
C(7, 3) = 35
Resultado:
O coeficiente do termo em x³ é 35.
🔹 8. Termo geral: encontrando qualquer termo da expansão
Um dos recursos mais poderosos do Binômio de Newton é a possibilidade de encontrar um termo específico da expansão sem precisar expandir tudo.
Essa técnica é muito usada em provas da ESA, EPCAR, EsPCEx, EEAR, Petrobras e concursos técnicos porque economiza tempo, evita erros e exige domínio real do conteúdo.
Para isso, utilizamos o termo geral do binômio.
Ele é a chave para acessar qualquer parte da expansão de (a + b)ⁿ de forma rápida e precisa. 🔑✨
📘 A fórmula do termo geral
O termo de ordem (k + 1) da expansão é dado por:
Tₖ₊₁ = C(n, k) · aⁿ⁻ᵏ · bᵏ
Cada elemento da fórmula tem um papel claro:
- C(n, k) → coeficiente do termo
- aⁿ⁻ᵏ → potência decrescente de a
- bᵏ → potência crescente de b
Essa fórmula funciona para qualquer binômio (a + b)ⁿ, independentemente dos valores de a, b ou n.
⭐ Exemplos claros e diretos
✔ 1. Encontrar o 4º termo da expansão de (a + b)⁶
Queremos o termo de ordem 4.
Logo:
k + 1 = 4 → k = 3
Aplicando o termo geral:
- C(6, 3) = 20
- a⁶⁻³ = a³
- b³
Resultado:
T₄ = 20a³b³
✔ 2. Encontrar o termo em x⁵ na expansão de (2x + 1)⁷
Queremos o termo cujo expoente de x é 5.
No termo geral:
(2x)⁷⁻ᵏ → x⁷⁻ᵏ
Para ser x⁵:
7 − k = 5
k = 2
Agora calculamos:
- C(7, 2) = 21
- (2x)⁵ = 32x⁵
- 1² = 1
Resultado:
T₃ = 21 · 32x⁵
T₃ = 672x⁵
Resposta:
O termo em x⁵ é 672x⁵.
✔ 3. Encontrar o termo independente em (x − 2)⁸
Termo independente = sem x.
No termo geral:
x⁸⁻ᵏ → expoente deve ser 0:
8 − k = 0
k = 8
Agora substituímos:
- C(8, 8) = 1
- x⁰ = 1
- (−2)⁸ = 256
Resultado:
O termo independente é 256.
✔ 4. Encontrar o termo com a²b³ em (a + b)⁵
A soma dos expoentes deve ser igual a n:
a² · b³ → expoentes 2 + 3 = 5 → válido
a⁵⁻ᵏ = a² → então:
5 − k = 2
k = 3
Coeficiente:
C(5, 3) = 10
Resultado:
O termo com a²b³ é 10a²b³.
🔹 9. Termo independente e maior coeficiente
Dentro das aplicações do Binômio de Newton, dois tipos de questões aparecem com enorme frequência em concursos:
o termo independente e o maior coeficiente da expansão.
Saber encontrá-los rapidamente faz toda a diferença em provas como ESA, EPCAR, EEAR, EsPCEx, Colégio Naval e Petrobras.
Vamos analisar cada um separadamente. 👇
⭐ 1. Termo Independente
O termo independente é aquele que não possui a variável, ou seja, um termo que é apenas número.
Esse tipo de questão cai muito porque exige compreensão profunda do termo geral.
📘 Fórmula base:
Tₖ₊₁ = C(n, k) · aⁿ⁻ᵏ · bᵏ
Para o termo ser independente, o expoente da variável deve ser zero.
✔ Exemplo 1: termo independente de (x − 2)⁸
O termo geral contém:
x⁸⁻ᵏ → queremos expoente 0.
Então:
8 − k = 0
k = 8
Agora substituímos:
- C(8, 8) = 1
- x⁰ = 1
- (−2)⁸ = 256
Resultado:
O termo independente é 256.
✔ Exemplo 2: termo independente de (2x + 3)⁵
O termo contém:
(2x)⁵⁻ᵏ → x⁵⁻ᵏ
Para desaparecer:
5 − k = 0 → k = 5
Agora calculamos:
- C(5, 5) = 1
- (2x)⁰ = 1
- 3⁵ = 243
Resultado:
O termo independente é 243.
✔ Exemplo 3: termo independente de (x/2 − 4)⁶
A variável está em (x/2)⁶⁻ᵏ → expoente deve ser 0:
6 − k = 0
k = 6
Cálculo:
- C(6, 6) = 1
- (x/2)⁰ = 1
- (−4)⁶ = 4096
Resultado:
O termo independente é 4096.
⭐ 2. Maior coeficiente da expansão
Uma das propriedades mais bonitas da expansão de (1 + x)ⁿ é que os coeficientes crescem até o centro e depois diminuem.
Isso significa que o maior coeficiente está próximo de:
k = n / 2
Ou exatamente no meio quando n é par.
📘 Para (1 + x)ⁿ:
- Se n é par, o maior coeficiente é C(n, n/2).
- Se n é ímpar, existem dois coeficientes iguais, nos termos:
- C(n, (n−1)/2)
- C(n, (n+1)/2)
Esse padrão aparece diretamente no Triângulo de Pascal.
✔ Exemplo 1: maior coeficiente de (1 + x)⁸
n = 8 → par
Maior coeficiente = C(8, 4)
C(8, 4) = 70
✔ Exemplo 2: maior coeficiente de (1 + x)⁵
n = 5 → ímpar
Coeficientes centrais:
- C(5, 2) = 10
- C(5, 3) = 10
Resultado:
O maior coeficiente é 10 (e ocorre duas vezes).
✔ Exemplo 3: maior coeficiente de (2 + x)⁹
Quando o binômio não é (1 + x), mas sim (a + b)ⁿ, os coeficientes numéricos continuam sendo C(n, k).
n = 9 → ímpar
Coeficientes centrais:
- C(9, 4) = 126
- C(9, 5) = 126
Maior coeficiente:
126
Obs.: O valor de a e b só influencia o termo final, NÃO o coeficiente numérico.
⭐ Por que isso cai tanto em concursos?
- Testa domínio do termo geral
- Avalia entendimento do Triângulo de Pascal
- Exige raciocínio rápido
- Evita expansão completa (que tomaria muito tempo na prova)
Quem domina esses conceitos resolve questões em menos de 20 segundos — uma vantagem enorme em provas objetivas.
🔹 10. Aplicações avançadas: conexão entre Binômio de Newton e Probabilidade Binomial
Depois que o estudante entende o Binômio de Newton, surge uma das aplicações mais importantes em concursos:
a Probabilidade Binomial, que aparece em provas da ESA, EsPCEx, EEAR, EPCAR, Colégio Naval, Petrobras e bancas como Cebraspe e Cesgranrio.
E o mais interessante é que a probabilidade binomial utiliza exatamente a estrutura do Binômio de Newton.
Isso faz com que um conteúdo complemente o outro naturalmente.
🎲 A ligação fundamental
Quando calculamos a probabilidade de um evento ocorrer várias vezes, usamos a fórmula:
C(n, k) · pᵏ · qⁿ⁻ᵏ
E isso é praticamente idêntico ao termo geral da expansão:
C(n, k) · aⁿ⁻ᵏ · bᵏ
Ou seja:
- p corresponde a uma parte do binômio
- q corresponde à outra parte
- C(n, k) é o coeficiente do Binômio de Newton
- k determina quantas vezes o evento ocorre
Por isso, dominar o binômio torna a probabilidade binomial MUITO mais fácil.
📌 Estrutura típica da Probabilidade Binomial
A probabilidade é usada quando:
✔ A experiência tem apenas 2 resultados (sucesso ou fracasso)
✔ A probabilidade permanece constante
✔ Os ensaios são independentes
✔ Há repetição de experimentos
Isso aparece em provas com frases como:
- “probabilidade de acertar X questões…”
- “probabilidade de conseguir sucesso Y vezes…”
- “probabilidade de um equipamento falhar exatamente k vezes…”
Tudo isso é Binômio de Newton disfarçado!
📘 Exemplo 1: probabilidade de acertos
Uma questão de concurso diz:
Um aluno acerta uma questão com probabilidade 0,7.
Qual a probabilidade de ele acertar exatamente 3 questões em 5 tentativas?
Estrutura binomial:
- n = 5
- k = 3
- p = 0,7
- q = 0,3
Aplicação direta:
C(5, 3) · (0,7)³ · (0,3)²
Agora basta calcular:
C(5, 3) = 10
(0,7)³ = 0,343
(0,3)² = 0,09
Resultado:
10 × 0,343 × 0,09 = 0,3087
Probabilidade = 30,87%
Repare como é a estrutura de um termo do binômio!
📘 Exemplo 2: falhas em um equipamento
Um equipamento falha com probabilidade 0,1.
Em 8 testes, qual a probabilidade de falhar exatamente 2 vezes?
- n = 8
- k = 2
- p = 0,1
- q = 0,9
Probabilidade:
C(8, 2) · (0,1)² · (0,9)⁶
C(8, 2) = 28
(0,1)² = 0,01
(0,9)⁶ ≈ 0,531441
Cálculo:
28 × 0,01 × 0,531441 = 0,1488
Probabilidade ≈ 14,88%
Esse tipo de questão é clássica em provas da Cesgranrio e Cebraspe.
⭐ Por que isso é tão cobrado em concursos?
✔ Mistura raciocínio lógico + combinatória
✔ Exige rapidez com combinação simples
✔ Faz parte da modelagem probabilística moderna
✔ Está presente em simulados militares, bancários, engenharias e prova da Petrobras
Quem domina o Binômio de Newton já está 50% preparado para esse tipo de questão.
🔹 11. Exercícios comentados passo a passo
Aqui estão três exercícios que representam exatamente o que você encontra em provas de concursos como ESA, EsPCEx, EPCAR, EEAR, Colégio Naval, Instituto Militar de Engenharia e CESGRANRIO.
Cada exercício foi pensado para fixar conceitos essenciais do Binômio de Newton e suas aplicações modernas.
⭐ Exercício 1 — Nível Fácil
💬 Enunciado
Encontre o terceiro termo da expansão de:
(x + 2)⁵
📘 Resolução
Usamos o termo geral:
Tₖ₊₁ = C(n, k) · aⁿ⁻ᵏ · bᵏ
Aqui:
- n = 5
- a = x
- b = 2
- Terceiro termo → k = 2
Agora substituímos:
1️⃣ C(5, 2) = 10
2️⃣ x⁵⁻² = x³
3️⃣ 2² = 4
Então:
T₃ = 10 · x³ · 4 = 40x³
✔ Resposta:
40x³
⭐ Exercício 2 — Nível Médio
💬 Enunciado
Qual é o termo independente da expansão de:
(2x − 3)⁶
📘 Resolução
O termo independente é aquele em que não aparece x.
O termo geral contém:
(2x)⁶⁻ᵏ → x⁶⁻ᵏ
Queremos:
6 − k = 0 → k = 6
Agora substituímos no termo geral:
1️⃣ C(6, 6) = 1
2️⃣ (2x)⁰ = 1
3️⃣ (−3)⁶ = 729
✔ Resposta:
729
⭐ Exercício 3 — Nível Difícil (Estilo Cesgranrio / EsPCEx / EPCAR)
💬 Enunciado
Considere o desenvolvimento de:
(1 + x)¹²
Qual é o maior coeficiente numérico presente na expansão?
📘 Resolução
Para binômios do tipo (1 + x)ⁿ, os coeficientes são exatamente os valores de:
C(n, k)
Para n = 12 (par), o maior coeficiente é:
k = 12 / 2 = 6
Então:
C(12, 6)
Agora calculamos:
C(12, 6) = 924
✔ Resposta:
924
🎯 Observações importantes para concursos
Esses três tipos de questões aparecem o tempo todo:
✔ Encontrar termos específicos
✔ Termo independente
✔ Maior coeficiente
E ao dominar esses padrões, você passa a resolver rapidamente — muitas vezes sem nem usar papel.
✈️📘 EPCAR: o que esperar das questões de matemática 🎯📊

🎯 1. A importância da matemática na prova da EPCAR
A matemática é o coração da prova da EPCAR — e não é exagero dizer que dominar essa disciplina pode ser o fator decisivo entre ser apenas mais um candidato ou conquistar a tão sonhada vaga. 💪📘
Na Escola Preparatória de Cadetes do Ar, a matemática ocupa posição de destaque, com peso elevado em relação a outras matérias. Ela é o verdadeiro termômetro da prova, capaz de medir não só o nível de conhecimento teórico, mas também a capacidade de raciocínio, rapidez e concentração do estudante. Cada questão é desenhada para testar o candidato em três dimensões: entendimento, lógica e estratégia.
🧠 Mais do que decorar fórmulas, a EPCAR quer saber se você pensa matematicamente. Isso significa interpretar problemas, encontrar padrões e escolher o caminho mais eficiente para chegar à resposta. As bancas da Aeronáutica valorizam a clareza nos cálculos, a organização do raciocínio e a habilidade de lidar com situações numéricas de forma ágil e precisa.
Além disso, o peso da matemática não é apenas estatístico — ele reflete a essência da formação militar e aeronáutica: disciplina, método e raciocínio sob pressão. ✈️⚙️
Por isso, quem domina essa matéria não apenas pontua mais, mas também mostra à banca que possui as características ideais de um futuro cadete do ar: foco, raciocínio rápido e equilíbrio emocional.
📈 Em resumo: se você quer decolar na EPCAR, precisa fazer da matemática sua principal aliada.
Treine todos os dias, resolva provas antigas e transforme os desafios numéricos em combustível para o seu voo rumo à aprovação. 🚀✏️
📊 2. Estrutura da prova e perfil das questões
A prova de Matemática da EPCAR é planejada para avaliar a essência do raciocínio lógico e a capacidade do candidato de aplicar a teoria de forma prática. 🎯 É uma prova que premia quem entende, não quem decora.
Geralmente, o exame apresenta múltiplas questões objetivas (em torno de 24 a 30), cada uma com cinco alternativas (A a E), e um tempo total aproximado de 4 horas para todas as disciplinas. Isso exige agilidade mental, estratégia e foco, pois o candidato precisa resolver problemas de forma precisa sem se perder nos detalhes. ⏱️
🧮 Nível de dificuldade progressivo:
A EPCAR costuma organizar as questões de forma inteligente — começando com exercícios mais diretos e conceituais, e aumentando gradualmente o nível de complexidade.
- As primeiras questões testam conceitos básicos, como operações, frações e proporções.
- As intermediárias cobram resolução de problemas contextualizados, exigindo mais interpretação e raciocínio.
- As últimas trazem situações desafiadoras, que envolvem análise combinatória, geometria espacial, funções e raciocínio algébrico avançado.
Esse formato exige que o aluno tenha ritmo e estratégia. O ideal é garantir os acertos nas questões fáceis e médias antes de investir tempo nas mais complexas. ⚡
📘 Estilo da banca (Comando da Aeronáutica):
As provas seguem um padrão rigoroso, com foco em:
- Clareza nos enunciados: sem textos longos, mas com alto poder interpretativo.
- Cálculos limpos e objetivos: a banca valoriza o raciocínio organizado, sem necessidade de decorações mirabolantes.
- Domínio de fundamentos: quem domina as bases matemáticas (frações, potências, proporcionalidade, equações e geometria) se destaca.
💡 Resumo estratégico:
A prova da EPCAR é um espelho do perfil militar: precisão, disciplina e eficiência.
Quem treina com foco, entende os conceitos e administra bem o tempo consegue transformar a matemática de vilã em aliada — e voar alto rumo à aprovação. ✈️📈
🔢 3. Principais conteúdos cobrados em matemática
Se há uma palavra que define a prova de Matemática da EPCAR, é constância. 📘✨ Ano após ano, os mesmos temas voltam a aparecer — com variações, contextos diferentes e níveis de profundidade que testam quem realmente domina o conteúdo. Saber o que mais cai é o primeiro passo para estudar com estratégia e evitar desperdiçar tempo com tópicos menos relevantes.
📚 Veja os conteúdos mais recorrentes nas provas da EPCAR:
✅ 1. Operações básicas e frações
Essenciais para os cálculos de toda a prova. A Aeronáutica cobra precisão e rapidez, então dominar operações com números racionais, frações e potências é obrigatório.
✅ 2. Expressões algébricas e equações (1º e 2º grau)
Um dos pilares da prova. Questões pedem para montar e resolver equações a partir de situações-problema, com foco em interpretação e agilidade.
✅ 3. Razão, proporção e regra de três
Sempre presentes, muitas vezes disfarçadas em problemas de física, geometria ou consumo. Saber aplicar a lógica proporcional é um diferencial para resolver as questões com segurança.
✅ 4. Porcentagem e juros simples/compostos
Temas que testam entendimento prático e aparecem em contextos de economia, descontos ou crescimento de valores.
✅ 5. Geometria plana e espacial
Clássico da EPCAR. Questões de áreas, perímetros, volumes e relações métricas (em triângulos e prismas) são frequentes. Exigem atenção às unidades e à visualização espacial. 📐
✅ 6. Trigonometria básica
O aluno deve conhecer relações fundamentais no triângulo retângulo, como seno, cosseno e tangente. O uso de fórmulas decoradas não basta — é preciso entender as razões e saber aplicá-las em diferentes situações.
✅ 7. Funções e gráficos
Aparecem de forma direta ou contextualizada, pedindo a interpretação de crescimento, decrescimento e comportamento gráfico. Um erro comum é tentar resolver sem analisar o gráfico — e é aí que muitos perdem pontos.
📈 Como priorizar o estudo:
- Use o Princípio de Pareto (80/20): 80% das questões estão concentradas em 20% dos conteúdos.
- Comece com equações, proporções, geometria e porcentagem — são os temas mais cobrados.
- Faça revisões semanais curtas com listas de exercícios mistos.
- Resolva provas antigas da EPCAR para reconhecer padrões e estilos de questão.
🎯 Resumo do comandante:
Na EPCAR, matemática é mais do que números — é disciplina e estratégia.
Quem entende os fundamentos, pratica com constância e aprende a reconhecer padrões, transforma qualquer questão difícil em oportunidade de pontuar alto. 🧮✈️
📈 4. O estilo das questões: interpretação e raciocínio
As provas de Matemática da EPCAR são conhecidas por um detalhe que diferencia os bons candidatos dos excelentes: a interpretação. 📖✏️
Mais do que aplicar fórmulas, o aluno precisa entender o que o problema realmente está pedindo — e é aí que a Aeronáutica mostra seu rigor.
Cada questão é elaborada para testar o raciocínio lógico, a atenção aos detalhes e a clareza de pensamento. O cálculo é importante, claro, mas o foco principal é a leitura inteligente do enunciado. Um pequeno erro de interpretação pode transformar uma questão fácil em uma armadilha difícil de escapar. ⚠️
💡 O segredo está na análise.
Muitos exercícios apresentam tabelas, gráficos, diagramas ou situações do cotidiano, como consumo de combustível, velocidade média, área de terreno ou economia doméstica. O candidato precisa extrair informações, relacioná-las e montar o raciocínio correto — quase como um detetive resolvendo um enigma numérico. 🕵️♂️🔢
📘 O que a EPCAR realmente quer medir:
- A capacidade de compreender textos matemáticos, transformando palavras em expressões numéricas.
- A habilidade de fazer inferências lógicas a partir de dados.
- O domínio de conceitos fundamentais (razão, porcentagem, equações, áreas, volumes) aplicados em contextos práticos.
E claro… sempre há as temidas “pegadinhas conceituais”. 😅
Algumas questões parecem simples, mas escondem erros sutis de interpretação, como trocar unidades, inverter razões ou confundir grandezas. A banca quer ver se o candidato pensa antes de calcular — se lê com atenção, confere o raciocínio e só depois parte para a operação.
🔍 Dica de ouro:
Antes de começar a resolver, sublinhe palavras-chave como “razão”, “diferença”, “aumentou”, “diminuiu”, “porcentagem”, “proporcional”.
Esses termos indicam exatamente o que a questão espera — e evitam que você caia nas distrações criadas propositalmente pela banca.
🎯 Em resumo:
A prova de matemática da EPCAR não é sobre velocidade, mas sobre precisão.
Quem lê com calma, organiza o raciocínio e entende o contexto, voa alto nas questões que derrubam a maioria. ✈️📊
🧠 5. Estratégias para resolver as questões com eficiência
Na prova de Matemática da EPCAR, saber o conteúdo é importante — mas saber jogar o jogo da prova é o que faz a diferença. 🎯
A banca cobra raciocínio, tempo de resposta e resistência mental. Por isso, o segredo está em combinar técnica, estratégia e prática. Vamos às armas do sucesso matemático: ⚔️📘
📖 1️⃣ Leitura atenta e sublinhar palavras-chave
Antes de colocar o lápis no papel, leia o enunciado com calma. A maioria dos erros na EPCAR não acontece por falta de conhecimento, mas por falha de interpretação.
🔹 Sublinhe termos importantes como “razão”, “diferença”, “aumentou”, “porcentagem”, “proporcional”, “quadrado”, “diâmetro”.
🔹 Identifique o que é dado, o que é pedido e o que está implícito.
💡 Isso ajuda o cérebro a organizar as informações e evitar distrações das “pegadinhas” da banca.
🧮 2️⃣ Simplifique cálculos e use estimativas inteligentes
Não caia na armadilha de resolver tudo da forma mais longa.
A EPCAR valoriza raciocínio prático e economia de tempo.
🔹 Verifique se o problema permite simplificar frações, eliminar termos repetidos ou fazer estimativas aproximadas.
🔹 Às vezes, uma boa análise lógica substitui várias linhas de conta.
💬 Exemplo: se uma razão envolve 2:4, simplifique para 1:2 antes de qualquer cálculo — e já elimine alternativas inconsistentes.
📚 3️⃣ Revisão rápida das fórmulas essenciais
Na véspera da prova, foque em um resumo visual com as fórmulas-chave:
- Equações: aₙ = a₁ + (n – 1)r; aₙ = a₁ × qⁿ⁻¹
- Geometria: áreas, perímetros e volumes mais cobrados.
- Trigonometria: seno, cosseno, tangente e relações no triângulo retângulo.
📘 Não tente decorar fórmulas novas de última hora — revise o que já domina.
⏱️ 4️⃣ Treino cronometrado com simulados anteriores da EPCAR
Nada substitui a prática real.
Monte simulados com questões oficiais dos últimos 5 anos, cronometre o tempo e simule as condições da prova.
🔹 Analise o tempo gasto por questão (ideal: 2 a 3 minutos).
🔹 Refaça as questões erradas e entenda onde o raciocínio falhou.
🔹 Repita até que o processo se torne natural — porque quem treina no limite, performa com tranquilidade. 💪
🎯 Resumo estratégico:
Leia com atenção.
Pense antes de calcular.
Simplifique sempre que possível.
Treine como se já estivesse no dia da prova.
Quem une técnica + calma + prática, transforma cada questão em uma oportunidade de pontuar alto e se destacar entre os melhores. 🚀✈️
📘 6. Erros mais comuns cometidos pelos candidatos
Todo candidato que sonha em vestir a farda da EPCAR precisa entender que a matemática da prova não é inimiga — ela é um teste de disciplina e atenção aos detalhes. 👀✈️
Por isso, saber quais erros mais derrubam candidatos é o primeiro passo para não cair nas mesmas armadilhas. Vamos direto ao ponto: ⚡
❌ 1️⃣ Pular etapas e errar por distração
O erro mais comum é a pressa. Muitos candidatos tentam “ganhar tempo” e acabam saltando etapas de cálculo ou pulando linhas importantes do raciocínio.
💡 Dica: escreva sempre as principais passagens do cálculo. Às vezes, um simples “zero” esquecido muda toda a resposta. A EPCAR adora testar atenção e organização.
❌ 2️⃣ Decorar fórmulas sem compreender o conceito
Memorizar sem entender é como pilotar um avião sem saber os comandos. 🚫
A prova exige raciocínio lógico e interpretação — se o aluno não entende por que usa determinada fórmula, acaba se perdendo quando o enunciado muda o formato da questão.
💬 Exemplo: usar a fórmula de área de triângulo sem perceber que o problema trata de um trapézio disfarçado.
✔️ Solução: estude o significado das fórmulas e treine a identificação do tipo de figura antes de aplicar o cálculo.
❌ 3️⃣ Falta de prática com frações, potências e unidades
Esses são os vilões silenciosos. 🧮
Pequenos deslizes em conversões de unidade, sinais de potência ou operações com frações custam pontos preciosos.
💡 Dica: reserve 10 minutos do seu estudo diário para revisar operações básicas — é nelas que a maioria dos candidatos tropeça.
❌ 4️⃣ Não administrar bem o tempo de prova
Alguns alunos gastam muito tempo em uma única questão, acreditando que precisam acertar tudo.
Resultado: deixam várias perguntas fáceis em branco. ⏱️
✔️ Solução: defina um limite de 3 minutos por questão. Se travar, pule e volte depois — às vezes, a mente clareia quando você muda o foco.
❌ 5️⃣ Ignorar o que o enunciado realmente pede
A EPCAR adora testar atenção.
Muitos candidatos resolvem a conta certa, mas respondem o valor errado, porque o enunciado pedia “a soma dos lados”, “a diferença entre as medidas” ou “o valor aproximado”.
⚠️ Dica: destaque com marca-texto (ou mentalmente) o verbo principal da questão — ele indica exatamente o que deve ser respondido.
✈️ Resumo de comandante:
“Na EPCAR, o erro não é não saber — é não perceber o que está na frente dos seus olhos.”
Treine com calma, revise seus erros e mantenha a mente focada.
Cada deslize corrigido é um passo mais próximo da sua aprovação.
A disciplina que você aplica agora será a mesma que te guiará nas asas da Aeronáutica. 🚀📘
🔍 7. Como a matemática da EPCAR se conecta com outros concursos militares
Estudar para a EPCAR é abrir as asas para um universo de oportunidades dentro do mundo dos concursos militares. ✈️📘
A base matemática cobrada na prova da Escola Preparatória de Cadetes do Ar é a mesma que sustenta o sucesso em outros certames como EEAR, EsPCEx, Colégio Naval e até concursos da Marinha e do Exército.
🧮 1️⃣ Similaridades entre os concursos militares
Os principais concursos das Forças Armadas seguem uma estrutura muito parecida:
- Questões conceituais e bem elaboradas, que testam raciocínio lógico e domínio de fundamentos.
- Ênfase em proporcionalidade, geometria, álgebra e funções, temas que são a espinha dorsal da EPCAR.
- Linguagem objetiva, sem “exageros teóricos”, mas com muita interpretação numérica e situações práticas.
Quem domina a matemática da EPCAR percebe que as provas da EEAR (Escola de Especialistas da Aeronáutica) e da EsPCEx (Escola Preparatória de Cadetes do Exército) seguem o mesmo padrão de raciocínio — mudam apenas o contexto e o grau de complexidade. 💡
📘 2️⃣ Estudar para EPCAR é construir uma base sólida para o futuro
A EPCAR forma estudantes que pensam com lógica, método e precisão, três qualidades exigidas em qualquer prova militar.
- O aluno que compreende a matemática da EPCAR tem facilidade para migrar entre provas e bancas diferentes.
- Os conteúdos de geometria, funções, progressões e trigonometria, por exemplo, são cobrados quase da mesma forma em todos os concursos militares.
- Isso significa que, ao se preparar bem agora, você já está adiantando metade do caminho para futuras aprovações. 🚀
📈 3️⃣ A vantagem de dominar a base matemática
Quando você domina os fundamentos, qualquer questão — seja de EPCAR, EEAR ou Colégio Naval — se torna apenas uma variação de algo que você já sabe resolver.
A matemática é cumulativa: o que você aprende hoje serve para sempre.
Quem entende razão e proporção, por exemplo, consegue resolver porcentagem, regra de três, funções e até problemas de física militar.
💬 Como dizem os veteranos:
“Quem conquista a EPCAR, conquista a base de todas as outras escolas militares.”
🎯 Resumo estratégico:
Estudar matemática para a EPCAR não é um fim — é um começo.
É o primeiro passo para dominar o raciocínio exigido por todas as forças armadas.
Cada questão resolvida é uma preparação para o próximo desafio, e cada acerto te aproxima de um futuro de excelência. 💪✈️
🚀 8. Rumo à aprovação
Chegar até aqui mostra que você está trilhando o caminho certo. 💪📘
Estudar para a EPCAR é mais do que se preparar para uma prova — é forjar o raciocínio, a disciplina e a mentalidade de um cadete do ar. Cada equação resolvida, cada simulado cronometrado e cada erro corrigido é um passo a mais rumo ao sonho de vestir o uniforme azul e representar a Força Aérea Brasileira. ✈️🇧🇷
A prova de matemática pode assustar no início, mas ela é justa com quem se prepara de forma inteligente.
O segredo não está em decorar fórmulas, e sim em entender o porquê de cada resultado.
É treinar com foco, revisar os fundamentos e, acima de tudo, acreditar que você é capaz de dominar o raciocínio matemático com paciência e constância.
🧠 Lembre-se:
A EPCAR procura jovens com lógica, estratégia e atitude — as mesmas qualidades que você está desenvolvendo a cada estudo.
A matemática não é um obstáculo, mas um trampolim que te impulsiona para um novo patamar de conhecimento e confiança.
📈 Dica final do comandante:
- Revise com regularidade.
- Faça simulados de anos anteriores.
- Corrija seus erros com humildade.
- E nunca perca o foco na missão.
Porque o verdadeiro aprovado não é aquele que acerta tudo de primeira, mas aquele que nunca desiste de tentar. 💥
✨ Equipe Você Aprovado 2005 deseja a você força, foco e fé nessa jornada.
Continue firme, mantenha o ritmo e lembre-se:
“A cada cálculo resolvido, você está um passo mais perto de voar alto.” 🛫📚
-

 Matemática para Concursos🎯4 meses ago
Matemática para Concursos🎯4 meses ago🧮 O que mais cai de matemática na ESA, EEAR e EPCAR
-

 Dicas de Estudos💡4 meses ago
Dicas de Estudos💡4 meses ago📅🚀 Reta Final: Como Revisar de Forma Inteligente e Turbinar Seu Desempenho na Prova 🧠💪🔥
-

 Editais e Concursos 📄7 meses ago
Editais e Concursos 📄7 meses ago🪖 Como se preparar para o concurso da ESA 2025
-

 Matemática pelo Mundo 🌎3 meses ago
Matemática pelo Mundo 🌎3 meses ago📘 SAT: The Exam That Opens Doors to U.S. Universities — A Complete Guide for Brazilians and Immigrants
-

 Editais e Concursos 📄7 meses ago
Editais e Concursos 📄7 meses ago🚒Concurso do Corpo de Bombeiros 2025 – Conheça o Certame 📄! 📢📚🔥
-

 Editais e Concursos 📄7 meses ago
Editais e Concursos 📄7 meses ago🚨 Edital / Concurso CBMERJ 2025 – Soldado BM (Busca e Salvamento)
-
 Dicas de Estudos💡4 meses ago
Dicas de Estudos💡4 meses ago📌 1. “Estudar Menos, Render Mais: Como o Método Pomodoro Pode Mudar Sua Rotina”
-

 Matemática pelo Mundo 🌎7 meses ago
Matemática pelo Mundo 🌎7 meses ago🇭🇺🎓 O segredo do ensino de matemática na Hungria 💡🔢
