📘Teoria dos Conjuntos
🔹 Definição de Conjunto
Um conjunto é uma coleção de elementos bem definidos, como números, letras ou objetos.
- Representado entre chaves { }.
- Nomeado por letras maiúsculas: A, B, C…
👉 Exemplo:
A = {a, b, c}
B = {0, 2, 4, 6}
🔹 Pertinência (∈ e ∉)
- Se um elemento pertence a um conjunto, usamos ∈.
- Se não pertence, usamos ∉.
👉 Exemplo:
A = {1, 2, 3}
1 ∈ A
4 ∉ A
🔹 Inclusão (⊂, ⊄)
Um conjunto é subconjunto de outro quando todos os seus elementos pertencem ao outro.
👉 Exemplo:
A = {−1, 2, 3, 7, 9}
B = {2, 7}
B ⊂ A
Se pelo menos um elemento de B não estivesse em A, diríamos B ⊄ A.
🔹 Igualdade de Conjuntos
Dois conjuntos são iguais se possuem os mesmos elementos, mesmo em ordem diferente.
👉 Exemplo:
A = {1, 2, 3}
B = {3, 2, 1}
A = B
🔹 Representações de Conjuntos
- Enumeração → listar elementos.
- Ex.: V = {a, e, i, o, u}
- Propriedade → usar condição.
- Ex.: P = {x | x é par menor que 10} = {0, 2, 4, 6, 8}
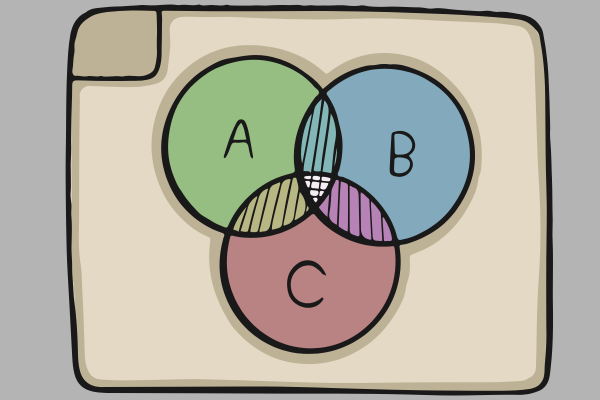
- Diagramas de Venn → círculos que mostram uniões e interseções.
🔹 Operações com Conjuntos
- União (∪) → elementos que estão em A ou B.
- 👉 Ex.: {1,2} ∪ {2,3} = {1,2,3}
- Interseção (∩) → elementos que estão em A e B.
- 👉 Ex.: {2,4,6} ∩ {2,3,5,7} = {2}
- Diferença (A − B) → elementos que estão em A, mas não em B.
- 👉 Ex.: A = {1,2,3,4,5,6}, B = {1,3,5} → A − B = {2,4,6}
- Complementar (Aᶜ) → elementos do universo U que não estão em A.
👉 Ex.: U = {1,2,3,4,5}, A = {2,3} → Aᶜ = {1,4,5}
🔹Conjunto Complementar (Importante!!!)
Definição – Seja U o conjunto universo (todos os elementos considerados em um problema).
O complementar de A, denotado por Aᶜ, é o conjunto de todos os elementos que estão em U mas não pertencem a A.
👉 Fórmula:
Aᶜ = U − A
🔹 Exemplo Básico
Universo: U = {1,2,3,4,5,6,7,8,9,10}
Conjunto: A = {2,4,6,8,10}
Complementar:
Aᶜ = U − A = {1,3,5,7,9}
📌 Ou seja, tudo o que não está em A, mas faz parte do universo U.
🔹 Propriedades Importantes
- (Aᶜ)ᶜ = A
- Uᶜ = ∅
- ∅ᶜ = U
- (A ∪ B)ᶜ = Aᶜ ∩ Bᶜ (Lei de De Morgan)
- (A ∩ B)ᶜ = Aᶜ ∪ Bᶜ (Lei de De Morgan)
🔹 Exemplo em Problema Estilo CESGRANRIO
Questão (adaptada)
Em uma pesquisa com 100 funcionários de uma refinaria, 70 afirmaram praticar esportes regularmente (conjunto E) e os demais não praticam. Quantos pertencem a Eᶜ?
a) 20
b) 25
c) 30
d) 35
e) 40
👉 Resolução:
Universo U = 100.
E = 70.
Eᶜ = U − E = 100 − 70 = 30.
✅ Gabarito: c) 30
🔹 Aplicação em Operações Industriais
Na área da Petrobras, problemas de conjuntos aparecem para representar grupos de equipamentos, pessoas ou processos.
- A = bombas em operação.
- U = todas as bombas instaladas.
- Aᶜ = bombas que não estão em operação (paradas ou em manutenção).
Isso permite interpretar rapidamente situações de disponibilidade ou falha.
🔹 Conjuntos Disjuntos
Dois conjuntos são disjuntos quando não têm elementos em comum.
👉 Exemplo:
A = {10,20,30}
B = {40,50}
A ∩ B = ∅
🔹 Conjunto Universo (U) e Conjunto Vazio (∅)
Universo (U): conjunto de todos os elementos do problema.
- 👉 Ex.: U = {1,2,3,4,5,6,7,8,9,10}
- Vazio (∅): conjunto sem elementos.
- 👉 Ex.: Conjunto dos números pares entre 3 e 5 → ∅
- 🔹 Princípio da Inclusão-Exclusão
Usado para contar elementos em uniões sem repetir os que estão em interseção.
📌 Fórmula para três conjuntos:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) − n(A ∩ B) − n(A ∩ C) − n(B ∩ C) + n(A ∩ B ∩ C)
👉 Exemplo:
Em uma turma:
- 20 estudam Matemática (A)
- 15 estudam Física (B)
- 10 estudam ambos (A ∩ B)
Quantos estudam Matemática ou Física?
n(A ∪ B) = 20 + 15 − 10 = 25
Questão 01 (CESGRANRIO – Petro)
Em um universo U com |U| = 500, sejam A, B e C três subconjuntos tais que |A| = 250,
|B| = 220, |C| = 200, |A ∩ B| = 120, |A ∩ C| = 100, |B ∩ C| = 90 e |A ∩ B ∩ C| = 60. O número de elementos fora de A ∪ B ∪ C é:
a) 40 b) 50 c) 60 d) 70 e) 80
Resolução
Dados: |U| = 500, |A| = 250, |B| = 220, |C| = 200, |A ∩ B| = 120, |A ∩ C| = 100, |B ∩ C| = 90,
|A ∩ B ∩ C| = 60.
Inclusão–Exclusão
|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B ∩ C|
= 250 + 220 + 200 − 120 − 100 − 90 + 60
= 420.
|U| = 500 e |A ∪ B ∪ C| = 420.
Assim, “fora de A ∪ B ∪ C” significa quantos elementos existem em U que não pertencem a A, nem a B, nem a C.
Conta:
500 − 420 = 80.
✅ Então, 80 elementos estão fora de A ∪ B ∪ C.
✅ Resumo Essencial para Concursos (como Petrobras – CESGRANRIO)
- Saber identificar pertinência (∈, ∉), inclusão (⊂, ⊄) e igualdade de conjuntos.
- Dominar as operações: união, interseção, diferença, complementar.
- Interpretar e resolver problemas com Diagramas de Venn.
- Aplicar o Princípio da Inclusão-Exclusão em problemas de contagem.
- Atenção a conjuntos disjuntos e ao conjunto vazio.
🧠 SABE O QUE É UM APÓTEMA?
Você já ouviu essa palavra em sala de aula e pensou:
“Isso vai cair na prova…” 👀
Pois saiba que apótema é um dos conceitos mais importantes da geometria plana, especialmente para quem estuda para ESA, EEAR, EPCAR, CFN e concursos militares.
E hoje você vai entender de forma clara, visual e aplicável.
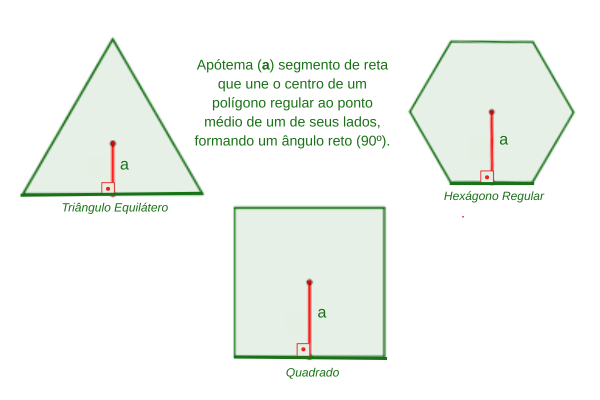
📌 1️⃣ O QUE É APÓTEMA?
A apótema é o segmento que liga o centro de um polígono regular até o ponto médio de um de seus lados, formando um ângulo de 90°.
Em termos simples:
✔ É a distância do centro até o lado.
✔ É sempre perpendicular ao lado.
✔ Só existe formalmente em polígonos regulares.
📐 2️⃣ POR QUE O TRIÂNGULO EQUILÁTERO É ESPECIAL?
Vejam todos os Pontos Notáveis existentes :
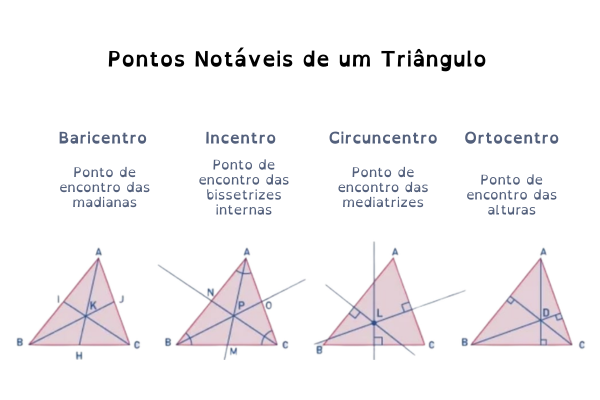
Baricentro (K) – é o ponto de encontro das três medianas de um triângulo, representando seu centro de gravidade ou centro de massa. Ele divide cada mediana na proporção de 2:1 (a parte do vértice é o dobro da parte do ponto médio) e está sempre no interior do triângulo.
- Incentro (P) – é o ponto notável de um triângulo formado pela intersecção das suas três bissetrizes internas, representando o centro da circunferência inscrita (tangente aos três lados)
- Circuncentro (L) – é o ponto de encontro das mediatrizes (retas perpendiculares nos pontos médios) dos lados de um triângulo, sendo o centro da circunferência que circunscreve o polígono e equidistante dos seus três vértices.
- Ortocentro – é o ponto de interseção das três alturas de um triângulo, onde cada altura é o segmento perpendicular que liga um vértice ao lado oposto.
Isso faz com que o estudo da apótema fique muito mais elegante, porque em um triângulo retângulo acontece algo incrível:
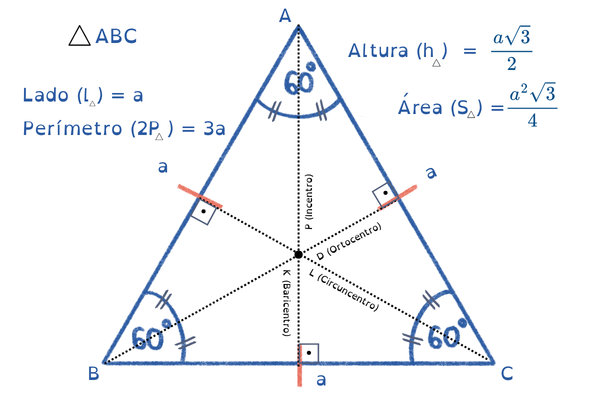
- O ponto de encontro da mediana, altura, bissetriz e mediatriz, coincidem no mesmo ponto.
🔥 3️⃣ RELAÇÃO ENTRE ALTURA E APÓTEMA
Altura do triângulo equilátero:
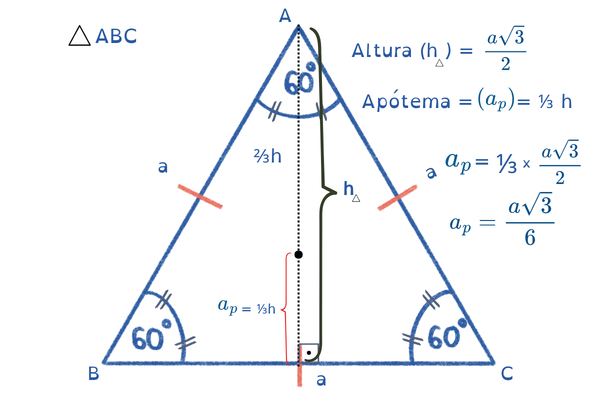
👉 A apótema é 1/3 da altura.
Essa é uma das pegadinhas favoritas de concurso.
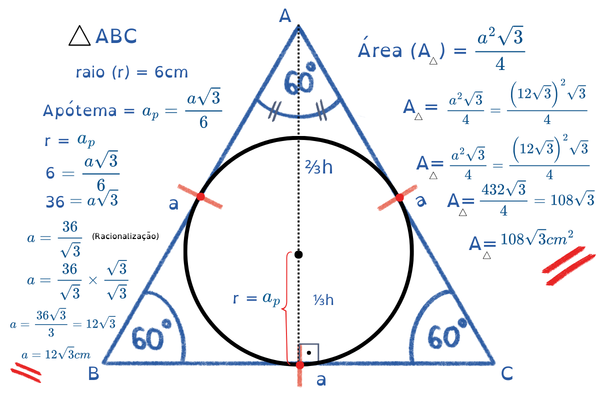
🚀 APLICAÇÃO 1
Circunferência INSCRITA no triângulo equilátero, encontre o lado (a) e a área (A) do triângulo equilátero.
Dado: r = 6 cm

🚀 APLICAÇÃO 2
Circunferência CIRCUNSCRITA ao triângulo equilátero, encontre o lado (a) e área (A)
Agora vamos inverter o raciocínio.
Raio da circunferência circunscrita (r): r = 8 cm
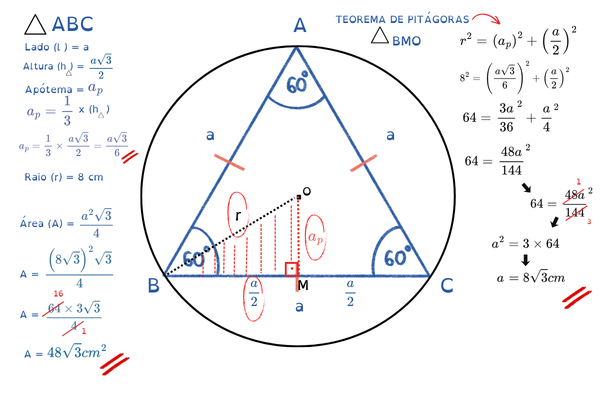
⚔️ DIFERENÇA IMPORTANTE PARA CONCURSOS
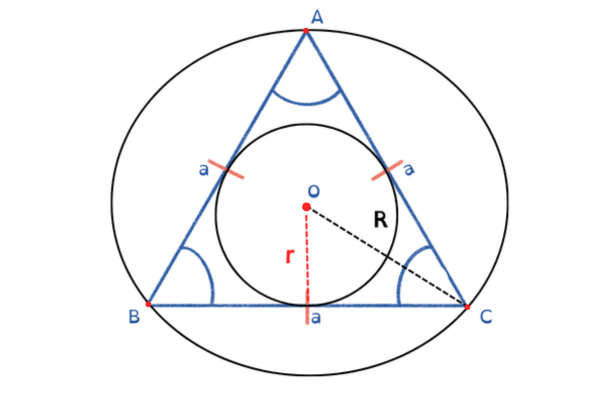
👉 A circunferência inscrita fica dentro do triângulo, tangenciando os três lados.
⚔️ DIFERENÇA QUE CAI EM PROVA MILITAR
🎯 Triângulo Equilátero
Existe uma diferença MUITO importante entre:
🔵 Circunferência Inscrita
🔴 Circunferência Circunscrita
E a banca AMA confundir isso.
🔵 1️⃣ CIRCUNFERÊNCIA INSCRITA
👉 Fica dentro do triângulo
👉 Toca os três lados
📌 Fórmula do raio (r):
r = (a√3) / 6
Onde:
a = lado do triângulo
💡 Relação com a altura
Altura do triângulo equilátero:
h = (a√3) / 2
Observe:
r = h / 3
⚠️ A apótema é 1/3 da altura.
Essa é pegadinha clássica.
🔴 2️⃣ CIRCUNFERÊNCIA CIRCUNSCRITA
👉 Fica por fora do triângulo
👉 Passa pelos três vértices
📌 Fórmula do raio (R):
R = (a√3) / 3
🔥 3️⃣ RELAÇÃO QUE DESPENCA EM PROVA
Temos:
r = (a√3) / 6 => r = R/2 => R = 2r
R = (a√3) / 3
🚨 CONCLUSÃO IMPORTANTE
🔴 O raio da circunferência circunscrita é o DOBRO do raio da inscrita.
Se a banca der:
• o valor de r → você multiplica por 2 para achar R
• o valor de R → divide por 2 para achar r
📚 QUER TREINAR AGORA?
Preparamos uma lista especial com questões nível ESA, EEAR e CFN envolvendo:
✔ Apótema
✔ Circunferência inscrita
✔ Circunferência circunscrita
✔ Área
✔ Relação entre alturas
👉 Vá agora na categoria “Baixe Aki” do blog e faça o download gratuito.
Treinar é o que transforma teoria em aprovação.
💡 CONCLUSÃO
Apótema não é apenas um segmento geométrico.
É uma ferramenta estratégica para:
- Resolver áreas rapidamente
- Evitar pegadinhas
- Ganhar tempo de prova
- Resolver questões de nível militar
Se esse conteúdo te ajudou, compartilhe com alguém que está estudando para concurso.
E continue acompanhando o blog.
Porque aqui, você aprende para passar.
Conceito e aplicação de Logaritmo
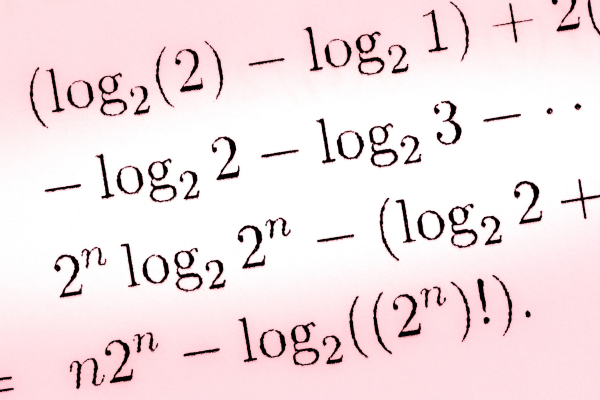
🔹 1️⃣ A Matemática por trás do Logaritmo: o Poder de Simplificar ✨
📘 O logaritmo é uma das invenções mais brilhantes da história da Matemática — ele nasceu para transformar multiplicações e potências em somas, tornando cálculos complexos muito mais fáceis!
💡 De forma intuitiva, pense assim:
👉 O logaritmo é o expoente que faz uma potência funcionar.
Por exemplo: log₂(8) = 3, pois 2³ = 8. Simples assim! 🔥
🧮 Antes das calculadoras, os cientistas e navegadores usavam tabelas de logaritmos para economizar tempo e evitar erros em cálculos enormes.
Hoje, ele continua sendo essencial para resolver problemas de crescimento exponencial, juros compostos, escalas sonoras e intensidade luminosa, além de aparecer em questões de concursos que exigem raciocínio e agilidade. 🚀
🎯 Dominar logaritmos é entender a linguagem das potências e das variações rápidas — e isso te coloca à frente em qualquer prova! 💪📚
🔹 2️⃣ Breve História e Origem do Conceito 🕰️
🌍 Tudo começou no século XVII, quando o matemático escocês John Napier teve uma ideia genial: criar uma forma de simplificar cálculos enormes que exigiam horas de trabalho manual. Assim nasceram os logaritmos — uma verdadeira revolução matemática! ⚡
🚢 Na época, navegadores, astrônomos e engenheiros precisavam lidar com multiplicações e potências gigantescas, e os logaritmos transformaram tudo isso em somas simples, acelerando descobertas e viagens.
📖 Logo surgiram as tabelas logarítmicas e, mais tarde, as famosas réguas de cálculo, usadas por engenheiros e cientistas durante séculos — inclusive nas missões espaciais da NASA! 🚀
💡 Curiosidade: os logaritmos não só facilitaram a vida dos matemáticos do passado, como também abriram o caminho para os computadores e para a era digital moderna, onde tudo é baseado em potências e escalas logarítmicas. 🔢✨
🎯 Entender de onde veio esse conceito é perceber como a matemática é a base de toda a evolução científica e tecnológica que vivemos hoje!
🔹 3️⃣ Conceito Formal e Propriedades Fundamentais 📘
📐 Definição:
Se aᵇ = c, então logₐ(c) = b.
👉 Em outras palavras, o logaritmo responde à pergunta:
“Qual expoente devo aplicar na base a para obter o número c?”
💡 Exemplo:
Como 2³ = 8, podemos dizer que log₂(8) = 3.
⚙️ Principais propriedades dos logaritmos:
1️⃣ logₐ(1) = 0 → Toda base elevada a zero é igual a 1.
2️⃣ logₐ(a) = 1 → A base elevada a 1 resulta nela mesma.
3️⃣ logₐ(M × N) = logₐM + logₐN → Multiplicações viram somas.
4️⃣ logₐ(M ÷ N) = logₐM – logₐN → Divisões viram subtrações.
5️⃣ logₐ(Mⁿ) = n × logₐM → O expoente “desce” multiplicando.
📈 Interpretação geométrica:
O logaritmo é o inverso da função potência, ou seja, se elevar números faz crescer rapidamente, tirar o logaritmo desacelera esse crescimento, permitindo comparar grandezas enormes em escala reduzida e proporcional — algo essencial em gráficos, escalas sonoras (decibéis), terremotos (Richter) e crescimento populacional. 🌍📊
🎯 Dominar essas propriedades é o primeiro passo para resolver qualquer questão de logaritmos com confiança e rapidez em concursos! 💪
🔹 4️⃣ Bases Mais Utilizadas e Suas Aplicações 🌟
📊 Os logaritmos podem ter várias bases, e cada uma delas tem um papel importante no mundo real — da economia à computação, passando pela física e biologia. Vamos ver as mais usadas 👇
🔸 Base 10 — Logaritmo Decimal (log₁₀):
Usado em economia, engenharia e escalas de medição.
💰 Exemplo: escalas logarítmicas que medem intensidade sonora (decibéis), magnitude de terremotos (escala Richter) e pH em química.
➡️ Ideal quando lidamos com números muito grandes ou muito pequenos, pois facilita comparações em múltiplas ordens de grandeza.
🔸 Base e — Logaritmo Natural (ln):
A base e ≈ 2,718 aparece em crescimentos contínuos: juros compostos, populações, reações químicas e até em fenômenos físicos.
📈 É a linguagem da mudança natural e do tempo contínuo, muito usada em física, biologia e finanças.
🔸 Base 2 — Logaritmo Binário (log₂):
Essencial na computação e nos algoritmos 💻
Cada bit duplicado representa uma potência de 2 — é por isso que processadores, memórias e códigos binários são baseados nessa lógica.
🌍 Exemplos reais de aplicação:
- Escala de decibéis (som) 🎧
- Escala de pH (química) ⚗️
- Magnitude sísmica (terremotos) 🌋
- Escalas astronômicas (brilho das estrelas) 🌠
🎯 Entender as bases logarítmicas é entender como o mundo mede, compara e transforma fenômenos em números! 💡
🔹 5️⃣ Logaritmo em Concursos e Exames 🎯
📘 O tema logaritmo é presença garantida em provas militares e bancas tradicionais, como ESA, EEAR, EsPCEx, Colégio Naval, EPCAR e CESGRANRIO.
Essas provas adoram testar raciocínio lógico e domínio das propriedades, exigindo atenção aos detalhes e rapidez nos cálculos! ⚡
🔎 Veja como o assunto costuma aparecer:
1️⃣ Cálculo direto e mudança de base:
Questões pedem o valor de expressões como log₂(8) ou aplicam a fórmula de mudança de base, exigindo agilidade e conhecimento das potências.
2️⃣ Igualdade de logaritmos e propriedades inversas:
Provas pedem para resolver equações logarítmicas, onde você precisa usar a igualdade de bases e argumentos — um erro aqui e o chute é certo! 😅
3️⃣ Aplicações em crescimento e decaimento:
O logaritmo aparece em problemas de juros compostos, populações, decaimento radioativo e escalas exponenciais, cobrando interpretação e contextualização. 📈📉
🧠 Exemplo no estilo das bancas:
Se log₃(x) = 4, qual o valor de x?
👉 x = 3⁴ = 81 ✅
💪 Dominar logaritmos é dominar o raciocínio das potências, e isso pode garantir vários pontos na sua prova!
Assista até o final, pratique com os exemplos e venha evoluir rumo à aprovação! 🚀
#ProfElias #MatemáticaParaConcursos #Logaritmos #ConcursosMilitares #EEAR2025 #ESA2025 #EsPCEx #ColégioNaval #Cesgranrio #VocêAprovado2005 #RaciocínioLógico
🔹 6️⃣ Logaritmos e Crescimento Exponencial 🚀
📈 O logaritmo e a função exponencial são como dois lados da mesma moeda — um cresce rapidamente, o outro controla e desacelera esse crescimento. São inversos perfeitos! 🔄
💡 Conexão direta:
Se y = aˣ, então x = logₐ(y).
Ou seja, o logaritmo “traduz” o crescimento exponencial em algo mais fácil de entender e comparar.
🌍 Aplicações reais:
- 💰 Juros compostos: quanto tempo leva para o capital dobrar.
- 👩🔬 Decaimento radioativo: meia-vida de elementos químicos.
- 🌱 Crescimento populacional: previsão de aumento ao longo dos anos.
- 📊 Economia: análises de inflação e retorno de investimentos.
📊 Visualização gráfica:
A função exponencial explode rapidamente, enquanto o gráfico logarítmico cresce cada vez mais devagar — ele “freia” o aumento e transforma grandes variações em escalas comparáveis.
🎯 Dica de prova:
Se a questão parece envolver tempo, crescimento ou decaimento, e há potências ou taxas constantes, desconfie! Ela pode estar “escondendo” uma função logarítmica que precisa ser revelada para resolver o problema. 👀📘
🔥 Entender essa relação é o segredo para resolver questões de juros, porcentagem e progressão geométrica com segurança e rapidez!
🔹 7️⃣ Estratégias Práticas para Resolver Questões de Logaritmo 🧠✨
⚡ Passo a passo para dominar log em prova:
1️⃣ Organize a expressão
Antes de sair calculando, reescreva tudo usando as propriedades. Muitas expressões “assustadoras” viram contas simples quando você separa produto, quociente e potência.
Ex.: logₐ(M × N) = logₐM + logₐN.
2️⃣ Faça o expoente descer
Sempre que aparecer algo do tipo logₐ(Mⁿ), transforme em n × logₐM. Isso corta muito cálculo e te permite comparar termos rapidamente.
3️⃣ Reduza para uma única base
Se a questão tem log em bases diferentes, tente converter usando mudança de base:
logₐ(b) = log(b) / log(a).
Isso é MUITO cobrado em bancas como ESA, EsPCEx e CESGRANRIO.
4️⃣ Cuidado com dois erros clássicos 🚨
- Base tem que ser positiva e diferente de 1.
- O argumento (o número “de dentro” do log) TEM QUE SER positivo.
Se não respeitar isso, a expressão nem existe — e várias alternativas erradas em concurso exploram exatamente esse detalhe.
📘 Exercício-modelo (estilo banca):
Se log₂(x) = 5, qual é o valor de x?
➡ Passo 1: transforme em forma exponencial: 2⁵ = x
➡ Passo 2: calcule 2⁵ = 32
✅ Resposta: x = 32.
💡 Por que isso importa?
Porque nas provas militares (EEAR, ESA, Colégio Naval, CFN) e bancas como CESGRANRIO e FGV, logaritmo quase nunca aparece “puro”: ele vem misturado com potência, PG, porcentagem, crescimento.
Quem sabe aplicar as propriedades com segurança resolve em segundos. Quem não sabe… chuta.
🔥 Treine esse raciocínio até virar automático. É ponto garantido na prova. 💪📚
🔹 8️⃣ O Logaritmo no Mundo Moderno 🌍💻
✨ O logaritmo deixou de ser apenas um conceito matemático — ele é uma linguagem universal do crescimento e da informação. Está presente em praticamente tudo o que move o século XXI. ⚙️
🔬 Da Física à Tecnologia:
Os logaritmos são usados para medir intensidades, frequências e energias. Em acústica, eles medem o som em decibéis (dB) 🎧; na química, servem para o pH das soluções ⚗️; e na astronomia, ajudam a definir o brilho das estrelas 🌠.
💾 Na era digital:
Eles são a base de algoritmos, compressão de dados e criptografia — tecnologias que permitem armazenar, processar e proteger informações em escala global.
Em Big Data e inteligência artificial, logaritmos ajudam a entender como os dados crescem exponencialmente e como reduzi-los a padrões compreensíveis. 📊🤖
📈 Escalas logarítmicas e ordens de magnitude:
Graças aos logaritmos, conseguimos representar crescimentos gigantescos — como a população mundial, o poder dos processadores ou a propagação de vírus — em gráficos compreensíveis e comparáveis.
Eles transformam o impossível em mensurável. 🌍
💡 Reflexão final:
O logaritmo é mais do que uma operação — é a chave para entender o ritmo acelerado do nosso tempo.
Num mundo onde tudo cresce em escala exponencial, o logaritmo é o instrumento que nos permite enxergar, medir e compreender o progresso. 🚀
#ProfElias #MatemáticaParaConcursos #Logaritmos #Tecnologia #BigData #Criptografia #ConcursosMilitares #RaciocínioLógico #VocêAprovado2005 #MatemáticaNaVidaReal
🔹 9️⃣ Caminho para o Domínio do Tema 🧭✨
📚 Aprender logaritmos é uma jornada, e o segredo está em revisar de forma inteligente e visual!
Monte seus flashcards com as principais propriedades e fórmulas, crie resumos coloridos e diagramas que mostrem a relação entre potência e logaritmo — isso ajuda seu cérebro a fixar o conteúdo com muito mais rapidez. 🎨🧠
⚙️ Dica prática:
Relacione o logaritmo com potências e porcentagens compostas.
Por exemplo: o crescimento percentual contínuo (como juros compostos) segue a mesma lógica de uma função exponencial, e entender o logaritmo te permite descobrir o tempo ou a taxa oculta em problemas financeiros e de variação. 💰📈
🔗 Quer reforçar sua base?
Confira o artigo [Porcentagem: entenda, calcule e aplique em concursos], que mostra como o raciocínio proporcional é o alicerce para dominar logaritmos, PG e juros compostos. Essa conexão vai turbinar seu aprendizado! 🚀
💬 Mensagem motivacional – Equipe Você Aprovado 2005:
“Nenhum conteúdo é difícil quando você entende o propósito por trás dele.
Cada fórmula é uma ferramenta — e cada estudo é um passo rumo à sua farda, sua vaga e sua vitória. 💪📘
Acredite no processo, revise com estratégia e vá até o fim. Você nasceu pra conquistar isso!” 🔥
“Entender logaritmo é compreender o ritmo oculto do crescimento —
e quem entende o ritmo, controla o resultado.” 💡📘
💹 Redução Percentual: entenda, calcule e aplique com confiança

📊 1. O que é Redução Percentual e onde ela aparece no dia a dia
A redução percentual representa uma diminuição proporcional em relação a um valor inicial, ou seja, uma variação negativa expressa em porcentagem. 💡
Em vez de mostrar apenas “quanto se perdeu”, ela revela a intensidade dessa perda em relação ao total original, o que torna essa medida essencial em economia, estatísticas e, claro, nas provas de concursos públicos. 🧮📘
🔹 Conceito central:
Quando um valor inicial sofre uma queda, a redução percentual indica quanto essa queda representa do todo.
👉 Em termos matemáticos:
Redução (%) = (Valor inicial – Valor final) ÷ Valor inicial × 100
💬 Exemplo:
O preço de um produto caiu de R$ 200 para R$ 150.
A variação é de R$ 50.
➡️ (50 ÷ 200) × 100 = 25% de redução.
Isso significa que o novo valor é 75% do preço original, ou seja, o produto ficou um quarto mais barato. 📉
🔹 Diferença entre redução percentual e desconto absoluto:
É comum confundir esses conceitos, mas eles não são iguais.
- Desconto absoluto → mostra quanto foi retirado em valor monetário.
Ex.: desconto de R$ 50 sobre um produto de R$ 200. - Redução percentual → mostra quanto esse desconto representa do valor total.
Ex.: a queda de R$ 50 representa 25% de redução.
Em concursos, essa diferença é vital, pois muitas questões trocam os termos de propósito para confundir o candidato. ⚠️
🔹 Exemplos reais de redução percentual:
A redução percentual está por toda parte, mesmo quando não percebemos:
- 💰 Promoções comerciais: “Liquidação! Preços até 30% mais baixos.”
- 🏭 Custos empresariais: uma fábrica que reduziu seus gastos de R$ 80 mil para R$ 60 mil — redução de 25%.
- 🌡️ Estatísticas e ciências: queda na temperatura média, na taxa de desemprego ou na emissão de poluentes.
- 💡 Metas de economia doméstica: reduzir a conta de energia em 15% ao mês.
Perceba: em todos os casos, a redução percentual permite comparar proporções, e não apenas valores absolutos.
🔹 Presença nas provas de concursos:
As bancas — como CESGRANRIO, ESA, EEAR e EsPCEx — adoram questões que envolvem redução percentual, porque testam interpretação, raciocínio e domínio de porcentagem.
📘 Exemplo típico:
Uma empresa reduziu seus custos de R$ 120.000 para R$ 90.000.
Qual foi a redução percentual?
➡️ (120.000 – 90.000) ÷ 120.000 × 100 = 25% de redução. ✅
Essas questões parecem simples, mas exigem atenção à base de cálculo, algo que derruba muitos candidatos.
📈 Resumo estratégico:
“A redução percentual é o espelho das variações no mundo real.
Quem entende suas relações sabe medir quedas, comparar resultados e interpretar o movimento dos números.” 💪
Dominar esse conceito é o primeiro passo para enfrentar temas como aumento sucessivo, juros compostos, descontos comerciais e estatísticas financeiras — todos muito cobrados nas provas. 🚀
💡 2. A lógica por trás da redução percentual
Por trás de cada cálculo de redução percentual existe uma lógica simples, porém poderosa, que conecta porcentagem, raciocínio proporcional e análise de variação. 🧠✨
Mais do que decorar fórmulas, entender o porquê dos números é o que transforma esse tema em um verdadeiro atalho para resolver questões de concursos com segurança e rapidez.
🔹 O raciocínio essencial: pensar em partes de 100
Toda porcentagem é uma fração do total (100%).
Quando há uma redução, significa que algo foi subtraído desse todo.
💬 Exemplo intuitivo:
Se o preço de um produto é 100% (valor inicial) e há uma redução de 20%, o que sobra é 80% do valor original.
👉 Isso quer dizer que o novo valor equivale a 0,8 × valor inicial.
É exatamente por isso que usamos a fórmula:
Valor final = Valor inicial × (1 – taxa de redução)
📘 Exemplo prático:
Uma passagem de ônibus custa R$ 10,00.
Após uma redução de 15%, o novo preço será:
10 × (1 – 0,15) = 10 × 0,85 = R$ 8,50.
Perceba que o raciocínio “1 – taxa” representa o que resta depois da redução.
🔹 Visualizando o processo:
Imagine um gráfico de barras com altura total representando 100%.
Quando há uma redução de 25%, a barra diminui, restando 75% da altura original.
Essa visão ajuda o cérebro a compreender que redução não é subtração direta, mas proporcional. 📊
🔹 Cuidado com as pegadinhas de prova:
1️⃣ Usar o valor errado como base de cálculo.
As bancas adoram trocar o “antes” e o “depois”.
➡️ Lembre-se: a base sempre é o valor inicial.
2️⃣ Confundir “redução de 20%” com “vale 20%”.
Uma redução de 20% sobre 200 não é 20 reais — é 40.
👉 200 × 0,20 = 40 → novo valor = 160.
3️⃣ Esquecer o raciocínio composto.
Quando há duas reduções seguidas (ex.: 10% e depois 20%), não se somam as taxas.
Cada redução é aplicada sobre o valor já reduzido — assunto que veremos na seção 5. ⚙️
🔹 Interpretação matemática:
A lógica da redução percentual é, na verdade, um processo multiplicativo de ajuste.
- “(1 – taxa)” representa o fator de redução.
- Quanto maior a taxa, menor o fator.
- O valor final será sempre uma fração do valor original.
💬 Exemplo de raciocínio rápido (estilo ESA):
O preço de uma mercadoria caiu de R$ 400 para R$ 300.
Qual o fator de redução?
(300 ÷ 400) = 0,75 → 75% restante → redução de 25%. ✅
📈 Resumo estratégico:
“Entender a lógica é mais poderoso que decorar a fórmula.
A redução percentual é uma forma de ver o que resta, não apenas o que se perde.” 🔍
Domine o raciocínio “(1 – taxa)” e você resolverá qualquer questão de porcentagem — inclusive aquelas disfarçadas em contextos de economia, estatística, física e lucro líquido. 💪
🧮 3. Passo a passo para calcular a redução percentual
Calcular uma redução percentual é muito mais simples do que parece — basta entender o caminho entre o valor inicial e o valor final. 🧠💡
Esse tipo de cálculo é cobrado em provas de matemática financeira, raciocínio lógico e porcentagem, tanto em concursos militares (EEAR, ESA, EsPCEx) quanto em provas da CESGRANRIO e FGV.
A seguir, veja como dominar esse raciocínio de forma prática e definitiva. 🚀
🔹 1️⃣ Método direto com porcentagem
Este é o modo mais rápido e intuitivo.
Se você sabe o percentual de redução, basta multiplicar o valor inicial por (1 – taxa).
📘 Exemplo:
Um produto custava R$ 120 e teve redução de 25%.
➡️ Valor final = 120 × (1 – 0,25)
➡️ Valor final = 120 × 0,75 = R$ 90
💬 Interpretação: o preço agora é 75% do original — o que significa uma queda de 25%.
🔹 2️⃣ Método comparativo — quando a taxa é desconhecida
Esse método é ideal quando você sabe quanto caiu, mas precisa descobrir a porcentagem da redução.
📘 Exemplo:
Um celular custava R$ 2.000 e passou a custar R$ 1.500.
➡️ Queda = 2.000 – 1.500 = 500
➡️ Redução (%) = (500 ÷ 2.000) × 100
➡️ Redução = 25%
💡 Dica de prova: sempre divida a diferença pelo valor inicial, e nunca pelo valor final. Essa é uma das pegadinhas mais clássicas! ⚠️
🔹 3️⃣ Método visual com proporção
Se preferir pensar visualmente, use a regra de três:
| Valor inicial | 100% |
|---|---|
| Valor final | x% |
📘 Exemplo:
Um produto de R$ 80 caiu para R$ 64.
➡️ 80 → 100%
➡️ 64 → x%
x = (64 × 100) ÷ 80 = 80%
✅ Isso significa uma redução de 20% (100% – 80%).
🔹 4️⃣ Conversão entre frações, decimais e percentuais
Muitos candidatos perdem tempo tentando converter mentalmente.
Veja como simplificar:
- 10% = 0,1 = 1/10
- 20% = 0,2 = 1/5
- 25% = 0,25 = 1/4
- 50% = 0,5 = 1/2
💬 Dica: memorize essas equivalências e use-as para estimar rapidamente o resultado.
📘 Exemplo:
“Redução de 25%” → multiplique o valor inicial por 3/4.
Ex.: 240 × 3/4 = 180.
🔹 5️⃣ Erros comuns e como evitá-los
⚠️ Erro 1: somar reduções diretamente (ex.: 20% + 10% = 30%).
❌ Errado. Cada redução é aplicada sobre o novo valor.
⚠️ Erro 2: dividir pelo valor errado (final em vez de inicial).
❌ Isso muda completamente o resultado.
⚠️ Erro 3: esquecer o raciocínio de “restante” (1 – taxa).
❌ A fórmula não mostra o que se perdeu, e sim o que ficou.
📈 Resumo estratégico:
“O segredo da redução percentual não está no número que cai,
mas na proporção que permanece.” 🧩
Domine esses três métodos — direto, comparativo e visual — e você estará preparado para qualquer tipo de questão sobre reduções, descontos ou variações sucessivas.
💬 4. Diferença entre redução percentual e desconto comercial
Embora os termos redução percentual e desconto apareçam lado a lado em muitas situações, eles não significam exatamente a mesma coisa. 🧾⚖️
Ambos indicam diminuição, mas a forma como são usados e o contexto de aplicação muda completamente — e essa diferença é crucial nas provas de concursos.
🔹 O que é uma redução percentual?
A redução percentual é um conceito geral e matemático, usado para medir qualquer tipo de queda proporcional em relação a um valor inicial.
Ela serve para avaliar variações, comparar desempenho e analisar tendências.
📘 Exemplos:
- A população de uma cidade caiu de 50.000 para 47.500 → redução de 5%.
- A produção de uma fábrica passou de 1.000 para 800 unidades → redução de 20%.
- O consumo de energia de uma empresa caiu de R$ 4.000 para R$ 3.200 → redução de 20%.
➡️ Perceba que não há relação comercial — apenas comparação entre antes e depois.
🏷️ O que é um desconto comercial?
O desconto é uma aplicação prática da redução percentual no comércio.
Ele representa a redução no preço de venda de um produto ou serviço — algo direto, financeiro e visível ao consumidor.
📘 Exemplo:
Uma loja anuncia: “Desconto de 15% em todos os produtos!”
Se um item custa R$ 200, o novo valor será:
200 × (1 – 0,15) = 200 × 0,85 = R$ 170.
Aqui, a redução percentual é aplicada com finalidade comercial: atrair clientes e ajustar preços.
⚙️ Resumo da diferença prática:
| Situação | Tipo | Finalidade | Exemplo |
|---|---|---|---|
| 📉 Queda de população, temperatura, custos, consumo | Redução Percentual | Medir variação ou desempenho | “O gasto de energia caiu 10%.” |
| 🏷️ Promoção de loja, abatimento em compra | Desconto Comercial | Reduzir valor de venda ou pagamento | “Desconto de 10% à vista.” |
🎯 Resumo rápido:
Todo desconto é uma redução percentual, mas nem toda redução percentual é um desconto.
💡 Pegadinhas em concursos:
1️⃣ Troca de termos:
Bancas como CESGRANRIO e ESA costumam usar “redução” no lugar de “desconto” para testar a atenção.
👉 Exemplo: “Um produto teve redução de 25% no preço.” (É, na prática, um desconto comercial.)
2️⃣ Mudança de base de cálculo:
Algumas questões pedem a variação em relação ao preço original e outras, em relação ao novo preço.
➡️ Fique atento à expressão “em relação a”.
Exemplo:
O preço caiu de R$ 100 para R$ 80 → redução de 20%.
Mas, em relação ao novo preço (80), o valor original era 25% maior.
📈 Aplicações práticas nas provas:
- Redução percentual: aparece em temas de economia, energia, estatísticas, desempenho e produtividade.
- Desconto comercial: cai em questões de porcentagem, juros simples e lucro.
💬 Exemplo clássico (EEAR):
Uma mercadoria de R$ 500 teve desconto de 12%.
Qual o valor final pago?
➡️ 500 × 0,88 = R$ 440. ✅
📘 Resumo estratégico:
“A redução explica o fenômeno.
O desconto transforma o fenômeno em vantagem.” 💸
Saber diferenciar os dois é o que garante o acerto em questões conceituais e aplicadas.
Domine essa lógica e você nunca mais cairá nas pegadinhas de variação percentual! ⚡📊
📉 5. Reduções sucessivas: o perigo de somar percentuais
Esse é um dos erros mais clássicos cometidos por candidatos em provas de porcentagem. 😬
Quando um valor sofre duas reduções seguidas, muita gente comete o engano de somar as taxas percentuais, achando que o resultado é simples — mas não é! ⚠️
Na verdade, as reduções sucessivas são compostas, ou seja, a segunda redução incide sobre o valor já reduzido, e não sobre o original.
Entender essa lógica é o que separa quem acerta por sorte de quem domina o raciocínio matemático com segurança. 💡
🔹 O erro comum: somar reduções diretamente
Imagine o seguinte caso:
Um produto de R$ 100 tem duas reduções sucessivas de 10%.
A maioria pensa:
“10% + 10% = 20%, logo o preço final é R$ 80.” ❌
Mas isso está incorreto, pois a segunda redução de 10% ocorre sobre o novo valor, que já foi reduzido.
O cálculo correto é multiplicativo, não aditivo.
🔹 A forma correta: multiplicação de fatores
Quando há reduções consecutivas, o valor final é obtido por:
Valor final = Valor inicial × (1 – a) × (1 – b)
onde a e b são as taxas de redução em forma decimal.
📘 Exemplo:
Preço inicial: R$ 100
Reduções: 10% e 10%
➡️ Valor final = 100 × (1 – 0,10) × (1 – 0,10)
➡️ Valor final = 100 × 0,9 × 0,9 = R$ 81
💬 Portanto, o total de redução não foi 20%, mas 19%.
✅ Redução real = (100 – 81) ÷ 100 × 100 = 19%.
🔹 Exemplo prático com contexto de prova
Uma empresa reduziu o consumo de combustível em 20% em janeiro e novamente em 10% em fevereiro.
Qual foi a redução total ao fim dos dois meses?
➡️ Valor final = 1 × (1 – 0,20) × (1 – 0,10)
➡️ Valor final = 1 × 0,8 × 0,9 = 0,72
✅ Redução total = 1 – 0,72 = 28%.
🎯 Dica: note que as taxas (20% e 10%) somam 30%, mas a redução real foi 28%, pois a segunda taxa incidiu sobre um valor já menor.
🔹 Dica para identificar pegadinhas em concursos
As bancas (como CESGRANRIO, FGV e EsPCEx) adoram testar esse tipo de raciocínio, especialmente quando o enunciado diz algo como:
“Um preço foi reduzido duas vezes consecutivas…”
⚠️ Se aparecer “duas vezes” ou “sucessivamente”, já saiba:
👉 Não some as taxas! Multiplique os fatores!
💡 Dica extra:
Você pode simplificar o cálculo multiplicando os fatores mentalmente:
- Redução de 10% → fator 0,9
- Redução de 20% → fator 0,8
Multiplique: 0,9 × 0,8 = 0,72 → redução de 28%.
📈 Resumo estratégico:
“Somar percentuais é fácil — mas errado.
O acerto está em multiplicar os fatores e entender o efeito composto.” ⚙️
Compreender reduções sucessivas é fundamental para resolver questões de juros compostos, variação de preços e desempenho acumulado, todos temas frequentes em concursos. 🧠💪
🧠 6. Interpretação em gráficos e tabelas
Entender redução percentual em gráficos e tabelas é uma habilidade valiosa — e muito cobrada em concursos! 📊
As bancas adoram transformar questões numéricas em representações visuais, exigindo que o candidato interprete quedas, proporções e variações com atenção aos detalhes.
Saber “ler” essas reduções é tão importante quanto saber calculá-las. 👀📘
🔹 Como identificar reduções percentuais em gráficos
Os gráficos de barras e colunas são os mais usados para representar variações ao longo do tempo.
Quando uma barra é menor que a anterior, isso indica uma redução percentual, e a diferença entre suas alturas mostra quanto caiu em relação ao valor inicial.
💬 Exemplo prático:
Uma empresa apresentou o seguinte gráfico de faturamento anual:
| Ano | Faturamento (R$ mil) |
|---|---|
| 2023 | 500 |
| 2024 | 400 |
➡️ A variação foi de 500 para 400, ou seja, uma queda de 100.
Redução percentual = (100 ÷ 500) × 100 = 20%.
📉 O faturamento caiu 20% em relação ao ano anterior.
💡 Dica visual: imagine o valor inicial como uma barra de 100%.
Tudo o que falta na nova barra representa a redução proporcional.
🔹 Como interpretar reduções em tabelas comparativas
As tabelas mostram valores lado a lado — e o segredo está em identificar qual é o “valor base”.
O cálculo é sempre feito em relação ao valor anterior, nunca ao final.
📘 Exemplo de tabela:
| Mês | Produção (unidades) |
|---|---|
| Janeiro | 1.000 |
| Fevereiro | 850 |
| Março | 765 |
➡️ Redução de janeiro para fevereiro:
(1.000 – 850) ÷ 1.000 × 100 = 15%
➡️ Redução de fevereiro para março:
(850 – 765) ÷ 850 × 100 = 10%
Perceba que o percentual de março não se baseia em janeiro, e sim no mês anterior — é isso que as bancas testam! ⚠️
🔹 Erros comuns na leitura de gráficos e tabelas
🚫 Erro 1 – Somar percentuais de períodos diferentes:
Reduções sucessivas não se somam diretamente (como vimos antes).
🚫 Erro 2 – Usar o valor final como base de cálculo:
A base é sempre o valor inicial da comparação.
🚫 Erro 3 – Ignorar escalas e unidades:
Verifique se os valores estão em reais, milhares, milhões, porcentagem ou unidades — isso muda tudo no resultado.
🔹 Como os concursos cobram esse tipo de questão
📘 Exemplo (CESGRANRIO):
O número de inscritos em um curso caiu de 1.200 para 900.
Qual foi a redução percentual e o número de alunos que permaneceram?
➡️ (1.200 – 900) ÷ 1.200 × 100 = 25% de redução.
➡️ Restaram 75% dos alunos → 1.200 × 0,75 = 900.
✅ Questões assim exigem raciocínio duplo: interpretação + cálculo.
📈 Resumo estratégico:
“Os números contam a história, mas os gráficos mostram o impacto.” 🎯
Dominar a leitura de reduções em gráficos e tabelas torna você mais rápido e preciso em provas que envolvem raciocínio lógico, estatística e porcentagem.
Cada queda representada visualmente é uma oportunidade de aplicar a fórmula certa — e garantir o ponto! 💪📊
⚙️ 7. Redução percentual em contextos financeiros e de concursos
A redução percentual é uma das aplicações mais cobradas nas provas de matemática financeira e raciocínio lógico, pois aparece em situações do mundo real — como juros, inflação, impostos e custos de empresas. 💰📉
Saber aplicar o conceito corretamente é o que faz diferença entre um chute e um acerto certeiro.
🔹 1️⃣ Redução percentual em juros e rendimentos
Quando o juros ou rendimento diminui, falamos em uma redução percentual de taxa ou valor.
Esse tipo de variação é comum em questões sobre juros compostos ou investimentos.
📘 Exemplo:
Um investimento que rendia 12% ao ano passou a render 9%.
➡️ Redução percentual = (12 – 9) ÷ 12 × 100 = 25%
💡 Ou seja, o rendimento foi reduzido em um quarto do valor original.
Nas provas, as bancas costumam pedir o percentual da queda, não apenas a diferença.
🔹 2️⃣ Redução percentual e inflação
A inflação também pode apresentar queda na taxa de crescimento, e esse raciocínio é testado em questões de atualidades matemáticas e estatísticas.
📘 Exemplo:
A inflação caiu de 5% para 3%.
➡️ Redução percentual = (5 – 3) ÷ 5 × 100 = 40%
💬 Interpretação: a taxa inflacionária foi reduzida em 40%, não em 2 pontos percentuais.
É justamente aqui que muitas pessoas erram — ponto percentual ≠ percentual de variação. ⚠️
🔹 3️⃣ Redução de impostos ou custos
Nos contextos empresariais, a redução percentual serve para medir economia e eficiência.
📘 Exemplo:
Uma empresa reduziu seu custo de produção de R$ 80 mil para R$ 64 mil.
➡️ (80.000 – 64.000) ÷ 80.000 × 100 = 20% de redução.
Esse tipo de questão aparece em bancas como CESGRANRIO, ESA e EsPCEx, especialmente em problemas de otimização de recursos e análise de lucros.
🔹 4️⃣ Aplicações em raciocínio lógico e porcentagem reversa
Algumas questões pedem o valor original, a partir de uma redução conhecida — é o chamado raciocínio reverso.
📘 Exemplo (Estilo ESA):
Após uma redução de 25%, um produto passou a custar R$ 120.
Qual era o preço original?
➡️ Valor final = Valor inicial × (1 – 0,25)
➡️ 120 = Valor inicial × 0,75
➡️ Valor inicial = 120 ÷ 0,75 = R$ 160 ✅
💡 Dica:
Quando o problema traz o valor depois da redução, divida pelo fator que restou (1 – taxa) para voltar ao valor original.
🔹 5️⃣ Questão comentada (CESGRANRIO – Adaptada)
Uma empresa de transportes reduziu o consumo mensal de combustível de 12.000 L para 9.600 L.
Qual foi a redução percentual?
📘 Resolução:
Redução = (12.000 – 9.600) ÷ 12.000 × 100
Redução = (2.400 ÷ 12.000) × 100 = 20%
✅ Resposta: a empresa reduziu o consumo em 20%, economizando um quinto do total.
📈 Resumo estratégico:
“A redução percentual está em tudo: no lucro que cai, na taxa que diminui e até na nota que melhora em relação à anterior.”
Saber identificar o que foi reduzido, qual é a base de comparação e como aplicar o raciocínio reverso faz toda a diferença nas provas de CESGRANRIO, ESA, EEAR e EsPCEx.
📚 Quem domina esse tema tem vantagem em qualquer questão de porcentagem, finanças ou estatística. 💪
🎯 8. Estratégias rápidas para resolver questões de redução percentual
Quando você está em prova e o tempo está correndo ⏱️, não dá para parar e montar conta longa em cada questão. Você precisa de atalhos. Precisa de leitura inteligente. Precisa de raciocínio limpo. E é exatamente isso que vamos construir aqui. 💪📊
Vamos direto às armas práticas 👇
🔹 1️⃣ Métodos mentais de cálculo: reduções de 10%, 20%, 25% e 50%
Alguns percentuais aparecem toda hora em prova. Se você souber calculá-los de cabeça, você voa.
• Redução de 10%
Tire 1/10 do valor.
Ex.: 10% de 240 = 24 → novo valor = 240 – 24 = 216.
Atalho mental: “andar uma casa para a esquerda na vírgula”.
240 → 24 → subtrai.
• Redução de 20%
20% = duas vezes 10%.
Basta tirar 10%, depois tirar mais 10% do original.
Ex.: 20% de 150 → 10% é 15 → 20% é 30 → 150 – 30 = 120.
Atalho mental: 20% = 0,8 do original (multiplicar por 0,8).
• Redução de 25%
25% = um quarto.
Tire 1/4 do valor.
Ex.: preço 200 → 1/4 de 200 é 50 → novo preço = 150.
Atalho mental: multiplicar por 0,75 dá o mesmo resultado.
• Redução de 50%
Metade. Sem drama.
Ex.: 340 com 50% de redução → metade → 170.
Atalho mental: multiplicar por 0,5.
💡 Repare como todos esses atalhos têm a mesma ideia:
Em vez de calcular “quanto caiu”, pense direto em “quanto sobra”.
- Caiu 10% → sobra 90% → 0,9 × valor inicial
- Caiu 20% → sobra 80% → 0,8 × valor inicial
- Caiu 25% → sobra 75% → 0,75 × valor inicial
- Caiu 50% → sobra 50% → 0,5 × valor inicial
Isso é ouro em prova. ✨
🔹 2️⃣ Como usar estimativas para eliminar alternativas erradas
Nem sempre você precisa achar o valor EXATO para acertar a questão. Às vezes basta saber a faixa.
Exemplo:
Um produto custa R$ 500 e sofre redução de 22%.
22% de 500 é um pouco mais que 20% de 500.
20% de 500 = 100.
Então a queda real é um pouco acima de 100, tipo ~110.
Logo o novo preço será um pouco abaixo de 400. 🔎
Se as alternativas forem:
A) 455
B) 440
C) 395
D) 360
Você já pode descartar as duas primeiras (a redução não foi tão pequena) e a última (seria queda de quase 30%).
Mesmo sem fazer a conta completa, você ficaria entre 395 e 400 → Marca C. ✅
Isso economiza tempo e salva ponto.
Use esse truque sempre que:
- A banca dá múltipla escolha.
- A conta seria chata (percentual quebrado tipo 17%, 22%, 13%).
- Você está no fim da prova e precisa fechar rápido.
🔹 3️⃣ Converta percentuais em frações simples durante a prova
Alguns percentuais têm frações lindas. Quando você enxerga a fração, a conta fica MUITO mais rápida:
- 10% → 1/10
- 20% → 1/5
- 25% → 1/4
- 33⅓% → 1/3
- 50% → 1/2
- 75% → 3/4
Por que isso importa? Porque fração você calcula no olho.
Exemplo:
“Uma máquina consome 800 L de água por dia. A empresa quer reduzir esse consumo em 25%.”
25% = 1/4.
1/4 de 800 = 200.
Novo consumo = 800 – 200 = 600 L.
Nem precisou montar fórmula. Nem porcentagem decimal. Só fração. Rápido. Limpo. Sem estresse. ⚡
Dica de prova:
Se vir 12,5%, lembre que 12,5% = 1/8.
Isso cai em questões de produção e divisão de recursos.
🔹 4️⃣ Exercício-modelo resolvido passo a passo
Agora vamos juntar tudo num estilo bem parecido com o que cai em ESA / EEAR / EsPCEx 👇
Problema:
Uma loja vendia um equipamento por R$ 400.
Para atrair clientes, aplicou uma redução de 15%.
Na semana seguinte, deu mais 10% de redução sobre o novo preço.
Qual é o valor final de venda?
🚀 Passo 1: aplicar a primeira redução (15%).
15% de 400 = 0,15 × 400 = 60
Novo preço = 400 – 60 = 340
⚠ Observa: Você também poderia ter feito direto 400 × 0,85 = 340 (porque 1 – 0,15 = 0,85).
Esse é o jeitinho rápido.
🚀 Passo 2: aplicar a segunda redução (10%) sobre 340.
10% de 340 = 34
Novo preço = 340 – 34 = 306
⚠ Ou direto:
Preço final = 400 × 0,85 × 0,90
0,85 × 0,90 = 0,765
400 × 0,765 = 306
🔎 Agora vem a pegadinha que a banca AMA:
A redução total NÃO foi “15% + 10% = 25%”.
Vamos ver:
Preço caiu de 400 para 306 → queda de 94.
94 ÷ 400 × 100 = 23,5%
✅ A redução total foi 23,5%.
Ou seja: quem somou 15 + 10 e marcou 25%… errou. 😬
💬 Resumo para levar pra prova:
- Percentual comum? Use fator direto (0,9 / 0,8 / 0,75).
- Percentual feio? Estime e elimine alternativas.
- Percentual bonitinho? Transforme em fração (1/4, 1/5, 1/2…).
- Reduções seguidas? Multiplica fatores, não soma porcentagens.
Dominar isso é virar predador de questão de porcentagem. 🐍📉
É ponto garantido na sua aprovação.
🚀 9. Rumo ao domínio da porcentagem e suas variações
Chegou a hora de transformar conhecimento em resultado real de prova. 💪📘
Depois de entender os conceitos de redução, aumento e variação composta, o próximo passo é consolidar — revisar, praticar e automatizar.
Quem faz isso com método e estratégia se torna imune às pegadinhas das bancas.
🔹 1️⃣ Revise com o método 80/20
O Princípio de Pareto (80/20) é o seu melhor aliado no estudo inteligente.
Ele diz que 80% das questões de porcentagem vêm de 20% dos conceitos.
👉 Foco nesses pontos:
- Redução e aumento percentual
- Reduções sucessivas
- Porcentagem reversa (encontrar o valor inicial)
- Aplicações financeiras (juros e descontos)
💡 Como aplicar:
- Monte uma folha com as 4 fórmulas essenciais.
- Faça 5 exercícios por dia com tempo cronometrado.
- Marque os erros e anote o motivo — não apenas a resposta.
Constância supera intensidade. É isso que cria domínio. 🚀
🔹 2️⃣ Pratique com simulados e flashcards
Os simulados temáticos ajudam você a unir raciocínio + agilidade.
Intercale questões da EEAR, ESA, EsPCEx e CESGRANRIO, pois todas testam variações percentuais sob formatos diferentes.
📘 Como treinar com eficiência:
- Crie flashcards (cartões) com uma face contendo o enunciado e a outra com a resposta.
- Misture conceitos: “redução + aumento”, “duas reduções sucessivas”, “variação reversa”.
- A cada acerto, explique em voz alta o raciocínio — isso reforça a memorização.
💬 Exemplo de flashcard:
Pergunta: Um produto de R$ 200 teve redução de 25% e depois aumento de 10%. Qual o preço final?
Resposta: 200 × 0,75 × 1,10 = R$ 165,00.
Treinar assim cria reflexo matemático, e o tempo de resolução despenca. ⏱️
🔹 3️⃣ Conexão com o artigo complementar
Para aprofundar o aprendizado, leia também o artigo 👉
📎 [Porcentagem: entenda, calcule e aplique em concursos].
Lá, você verá como a porcentagem se conecta à razão, proporção e regra de três, formando o tripé que sustenta praticamente todas as questões matemáticas de concursos.
Dominar ambos os conteúdos é construir base sólida e completa para qualquer prova. 🧠📊
🔹 4️⃣ Mensagem motivacional da Equipe Você Aprovado 2005
“Quem domina a porcentagem entende o movimento dos números —
e vence qualquer questão.” 💪📘
Você não está apenas aprendendo contas.
Está aprendendo a enxergar padrões, antecipar resultados e tomar decisões rápidas.
É isso que transforma candidatos em aprovados. 🌟
Então siga firme, revise sempre e lembre-se:
📈 a matemática não é inimiga — é uma aliada poderosa na sua aprovação.
-

 Matemática para Concursos🎯4 meses ago
Matemática para Concursos🎯4 meses ago🧮 O que mais cai de matemática na ESA, EEAR e EPCAR
-

 Dicas de Estudos💡4 meses ago
Dicas de Estudos💡4 meses ago📅🚀 Reta Final: Como Revisar de Forma Inteligente e Turbinar Seu Desempenho na Prova 🧠💪🔥
-

 Editais e Concursos 📄7 meses ago
Editais e Concursos 📄7 meses ago🪖 Como se preparar para o concurso da ESA 2025
-

 Matemática pelo Mundo 🌎3 meses ago
Matemática pelo Mundo 🌎3 meses ago📘 SAT: The Exam That Opens Doors to U.S. Universities — A Complete Guide for Brazilians and Immigrants
-

 Editais e Concursos 📄7 meses ago
Editais e Concursos 📄7 meses ago🚒Concurso do Corpo de Bombeiros 2025 – Conheça o Certame 📄! 📢📚🔥
-

 Editais e Concursos 📄7 meses ago
Editais e Concursos 📄7 meses ago🚨 Edital / Concurso CBMERJ 2025 – Soldado BM (Busca e Salvamento)
-
 Matemática para Concursos🎯4 meses ago
Matemática para Concursos🎯4 meses ago👉 📐 Teorema dos Segmentos Tangentes: o segredo das tangentes iguais!
-
 Dicas de Estudos💡4 meses ago
Dicas de Estudos💡4 meses ago📌 1. “Estudar Menos, Render Mais: Como o Método Pomodoro Pode Mudar Sua Rotina”
