📈 1️⃣ Função Exponencial

🔹 Definição:

É toda função da forma:
f(x) = aˣ, com a > 0 e a ≠ 1.

➡️ O número a é chamado de base e x é o expoente.

🔹 Domínio e imagem:

• Domínio: todos os números reais (ℝ)
• Imagem: números reais positivos (f(x) > 0)

🔹 Comportamento:

• Se a > 1, a função é crescente
• Se 0 < a < 1, a função é decrescente

📊 Exemplo:

• f(x) = 2ˣ → cresce (a = 2 > 1)
• f(x) = (1/2)ˣ → decresce (a = 1/2 < 1)

🔹 Propriedades importantes:

1. a⁰ = 1
2. a¹ = a
3. aᵐ × aⁿ = aᵐ⁺ⁿ
4. aᵐ ÷ aⁿ = aᵐ⁻ⁿ
5. (aᵐ)ⁿ = aᵐⁿ
6. (ab)ⁿ = aⁿ × bⁿ

💡 Essas propriedades são muito cobradas em provas de raciocínio lógico e álgebra.

🔹 Exemplo prático 1:

Calcule f(3) na função f(x) = 2ˣ
👉 f(3) = 2³ = 8

🔹 Exemplo prático 2:

Compare os valores: 2⁵ e 2⁴ × 2
👉 2⁵ = 32 e 2⁴ × 2 = 16 × 2 = 32
✅ Iguais (mesma base, somam-se os expoentes).

🧠 Dica de prova:

Quando a base é menor que 1, o sentido da desigualdade se inverte.
Exemplo:
(1/2)ˣ > (1/2)ʸ → implica que x < y

💡 2️⃣ Equações Exponenciais

São aquelas em que a variável aparece no expoente.
O objetivo é igualar as bases.

📘 Exemplo:
2ˣ = 8
➡️ 8 = 2³ → logo, 2ˣ = 2³
✅ x = 3

📘 Exemplo 2:
3ˣ = 1/9
➡️ 1/9 = 3⁻² → logo, 3ˣ = 3⁻²
✅ x = -2

📊 3️⃣ Função Logarítmica

🔹 Definição:

O logaritmo é o expoente ao qual devemos elevar a base para obter um número.

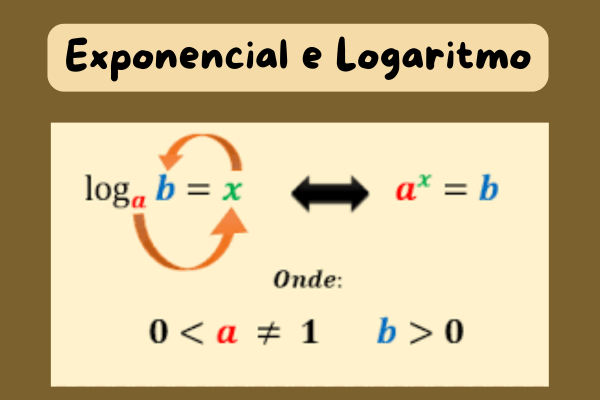
📘 logₐb = x ⇔ aˣ = b, com a > 0, a ≠ 1 e b > 0

➡️ Ou seja, o logaritmo “pergunta”:
“Qual expoente transforma a em b?”

💡 Exemplo:
log₂8 = ?
👉 2ˣ = 8 → x = 3
✅ log₂8 = 3

🔹 Domínio e imagem:

• Domínio: números positivos (b > 0)
• Imagem: todos os reais (ℝ)

🔹 Propriedades dos logaritmos:

1. logₐ1 = 0
2. logₐa = 1
3. logₐ(M × N) = logₐM + logₐN
4. logₐ(M ÷ N) = logₐM – logₐN
5. logₐ(Mⁿ) = n × logₐM
6. Mudança de base:
   logₐb = (log꜀b) ÷ (log꜀a)

💡 Exemplo prático:

log₃9 = ?
➡️ 3ˣ = 9 → 3ˣ = 3² → ✅ x = 2

📘 Outro exemplo:
log₅25 = ?
➡️ 5ˣ = 25 → 5ˣ = 5² → ✅ x = 2

⚙️ 4️⃣ Relação entre funções exponenciais e logarítmicas

Elas são funções inversas entre si.

📘 Se f(x) = aˣ, então sua inversa é f⁻¹(x) = logₐx.

💡 Isso significa que:

• aˣ = b ⇔ logₐb = x

🔁 Exemplo:
2³ = 8 ⇔ log₂8 = 3

📈 5️⃣ Gráfico das funções

🔹 Função exponencial (f(x) = aˣ):

• Passa pelo ponto (0,1).
• Crescente se a > 1
• Decrescente se 0 < a < 1

🔹 Função logarítmica (f(x) = logₐx):

• Passa pelo ponto (1,0).
• Crescente se a > 1
• Decrescente se 0 < a < 1
• Inversa da exponencial → são simétricas em relação à reta y = x

🧮 6️⃣ Aplicações em concursos

Esses temas aparecem em questões sobre:

• Crescimento populacional e juros compostos 📈
• Radioatividade e meia-vida ☢️
• Escalas logarítmicas (decibéis, pH, Richter) 🌋
• Raciocínio lógico e proporções geométricas 🧩

💬 7️⃣ Dicas finais da Equipe Você Aprovado 2005

✅ Sempre converta bases para o mesmo número, quando possível.
✅ Use logaritmo para “trazer o expoente para baixo” (em cálculos de juros compostos, por exemplo).
✅ Lembre-se: log e expoente são operações inversas — um desfaz o outro.
✅ Em provas, leia com calma: “a base”, “o número” e “o resultado” costumam causar confusão nas alternativas.

🏆 Resumo rápido

💙 Mensagem motivacional da Equipe Você Aprovado 2005:

“As funções exponenciais e logarítmicas ensinam algo além da matemática:
o que cresce com constância e base sólida, multiplica resultados.
Continue estudando, um passo de cada vez — e o seu sucesso também será exponencial.” 🚀📘💪

📌 1️⃣ Conceitos fundamentais

Capital (C):
É o valor inicial aplicado ou emprestado.
💡 Exemplo: investir R$ 1.000,00 é aplicar um capital de R$ 1.000,00.

Juros (J):
É a remuneração do capital — o “preço do dinheiro” no tempo.

Montante (M):
É o valor total após o período de aplicação.
📘 Fórmula: M = C + J

Taxa de juros (i):
É a porcentagem cobrada ou paga sobre o capital em um determinado período.

Tempo (n):
É o número de períodos da aplicação (dias, meses, anos).

🧮 2️⃣ Juros Simples

Nos juros simples, os juros são calculados sempre sobre o capital inicial.
A fórmula é direta e muito cobrada em concursos.

📘 Fórmulas:

• J = C × i × n
• M = C × (1 + i × n)

💡 Exemplo:
Um capital de R$ 2.000,00 é aplicado a 3% ao mês, durante 5 meses.
Calcule os juros e o montante.

👉 Solução:
J = 2.000 × 0,03 × 5 = R$ 300,00
M = 2.000 + 300 = R$ 2.300,00

🔹 Dica de prova: Sempre transforme a taxa percentual em decimal antes de aplicar (3% = 0,03).

📈 3️⃣ Juros Compostos

Nos juros compostos, os juros de cada período são acumulados ao capital, formando o novo valor base do cálculo.
É o famoso “juros sobre juros”, muito comum em bancos e financiamentos.

📘 Fórmulas:

• M = C × (1 + i)ⁿ
• J = M – C

💡 Exemplo:
Um capital de R$ 1.000,00 é aplicado a 10% ao mês por 3 meses.
Calcule o montante e os juros.

👉 Solução:
M = 1.000 × (1 + 0,10)³
M = 1.000 × 1,331 = R$ 1.331,00
J = 1.331 – 1.000 = R$ 331,00

🔹 Dica: Use a potência (1 + i)ⁿ — isso é o que diferencia os juros compostos dos simples.

📊 4️⃣ Taxas proporcionais e equivalentes

Taxas proporcionais:
Usadas em juros simples.
Exemplo: 12% ao ano → 1% ao mês (12 ÷ 12).

Taxas equivalentes:
Usadas em juros compostos (não são proporcionais).
Exemplo:
1% ao mês → taxa anual equivalente = (1 + 0,01)¹² – 1 = 0,1268 → 12,68% ao ano.

💱 5️⃣ Desconto Simples e Desconto Composto

➤ Desconto Simples (Comercial):

Quando se antecipa um pagamento antes do vencimento, o desconto é calculado sobre o valor nominal (N).
📘 Fórmula:
D = N × i × n
Valor Líquido (L) = N – D

💡 Exemplo:
Um título de R$ 2.000,00 é antecipado 3 meses antes do vencimento, com taxa de 2% ao mês.
D = 2.000 × 0,02 × 3 = R$ 120,00
L = 2.000 – 120 = R$ 1.880,00

➤ Desconto Composto:

Calculado sobre o valor atual do título, e não sobre o nominal.
📘 Fórmulas:
L = N × (1 – i)ⁿ
D = N – L

💡 Exemplo:
Título de R$ 1.000,00 antecipado por 2 meses à taxa de 5% a.m.:
L = 1.000 × (1 – 0,05)² = 1.000 × 0,9025 = R$ 902,50
D = 1.000 – 902,50 = R$ 97,50

🧾 6️⃣ Equivalência de capitais

Dois capitais são equivalentes quando têm o mesmo valor presente (ou futuro) em uma mesma data e à mesma taxa de juros.

📘 Fórmula genérica:
C₁ × (1 + i)ⁿ¹ = C₂ × (1 + i)ⁿ²

💡 Exemplo:
Qual deve ser o valor atual de R$ 1.210,00 vencível em 2 meses, à taxa de 5% ao mês?
C = 1.210 ÷ (1 + 0,05)² = 1.210 ÷ 1,1025 = R$ 1.098,00

💵 7️⃣ Valor Presente e Valor Futuro

Valor Presente (VP): o valor atual de um montante futuro.
Valor Futuro (VF): o valor que um capital terá no futuro.

📘 Fórmulas gerais (juros compostos):

• VF = VP × (1 + i)ⁿ
• VP = VF ÷ (1 + i)ⁿ

💡 Exemplo:
Quanto devo investir hoje para ter R$ 2.000 em 6 meses, com juros de 2% ao mês?
VP = 2.000 ÷ (1 + 0,02)⁶ = 2.000 ÷ 1,126 = R$ 1.776,00

🧠 8️⃣ Dicas rápidas para provas

✅ Leia atentamente o período da taxa: se for mensal e o tempo estiver em anos, converta!
✅ Atenção ao tipo de juros (simples ou compostos).
✅ Monte sempre o esquema C → J → M.
✅ Use estimativas para eliminar alternativas absurdas.
✅ Revise unidades de tempo e porcentagens.

🏆 Resumo visual final

💙 Mensagem da Equipe Você Aprovado 2005:

“Entender Matemática Financeira é dominar o tempo do dinheiro.
Cada fórmula é uma ferramenta — e quem sabe aplicá-las com confiança,
transforma números em conquistas.” 💪📘💰

🚫 1️⃣ O erro de copiar tudo ao invés de compreender

Um dos erros mais comuns dos estudantes é acreditar que resumir significa copiar. ✍️📄
Passar horas escrevendo o que o professor disse ou transcrevendo o PDF parece produtivo, mas na verdade é uma armadilha de falsa aprendizagem.
O cérebro não grava o que é repetido mecanicamente — ele grava o que é compreendido, processado e reconstruído com suas próprias palavras. 🧠💬

🎯 O resumo é uma síntese, não uma cópia

O verdadeiro objetivo de um resumo é filtrar o essencial, não reproduzir o conteúdo original.
Quando você escreve demais, gasta energia copiando e pouco tempo pensando.
O estudo se torna passivo, e o resumo vira apenas mais um texto decorado.

💡 Regra de ouro:

“Se o resumo parece o livro, você copiou.
Se parece a sua mente pensando, você aprendeu.”

🧩 Por que escrever demais causa cansaço e reduz a assimilação

Nosso cérebro tem um limite de atenção e processamento.
Ao tentar anotar tudo, você se sobrecarrega, perde o foco no raciocínio e não dá tempo para o cérebro refletir sobre o que está sendo aprendido.
Resultado: você entende durante a escrita, mas esquece logo depois.

✍️ É como tentar correr e anotar o caminho ao mesmo tempo — uma das duas tarefas vai sair mal feita.

🔁 Transforme o ato de resumir em um exercício de raciocínio

Em vez de copiar, interprete e reformule.
Ao ler um parágrafo, pergunte-se:

• “Qual é a ideia principal?”
• “Como eu explicaria isso para um colega?”
• “Posso simplificar esse trecho com um exemplo ou palavra-chave?”

Essas perguntas forçam seu cérebro a entender antes de escrever, ativando o aprendizado ativo.

📘 Exemplo prático

📍 Trecho original:

“A porcentagem é uma razão que compara um número com 100, usada para representar partes de um todo.”

📍 Resumo ineficiente:

“Porcentagem é uma razão que compara um número com 100, usada para representar partes de um todo.” (copiado!)

📍 Resumo inteligente:

“% → parte de 100 (comparação proporcional). Ex: 25% = 25/100.”

Viu a diferença?
Poucas palavras, ícones e uma estrutura que o cérebro reconhece rapidamente na revisão.

🎓 Mensagem para guardar:

“Copiar é repetir. Resumir é pensar.” 💭✍️

Quando você cria seu próprio resumo, transforma o conteúdo em conhecimento que pertence a você — e isso é o que realmente aparece na hora da prova. 🧠🔥

🧩 2️⃣ O erro de resumir sem propósito

Um dos maiores erros dos estudantes é resumir no automático, só porque ouviram dizer que “fazer resumo ajuda”. 📚💤
Sem um objetivo claro, o resumo vira um amontoado de frases bonitas — e não cumpre função nenhuma na hora da revisão ou da prova.
O segredo está em entender o porquê de cada resumo antes mesmo de começar a escrevê-lo. 🎯

💭 “Por que estou fazendo este resumo?”

Essa é a pergunta que deve guiar todo o processo.
Cada resumo precisa ter um propósito: fixar, revisar ou organizar ideias.
Quando você define a função, muda completamente a forma de escrever, o nível de detalhe e até o tempo investido.

💡 Lembre-se:

“Resumo sem propósito é como bússola sem norte — parece útil, mas não leva a lugar nenhum.” 🧭

🧠 Os 3 tipos de resumo e quando usá-los

1️⃣ 📖 Resumo de Leitura (primeiro contato)

• Serve para entender o conteúdo pela primeira vez.
• Ideal para matérias novas ou complexas.
• Deve conter explicações simples e exemplos básicos.
  🕒 Momento ideal: início dos estudos.

2️⃣ 🧠 Resumo de Revisão (reforço de memória)

• Focado em palavras-chave, fórmulas e esquemas curtos.
• Deve ser compacto e rápido de reler.
  🕒 Momento ideal: 1 a 7 dias após o estudo.

3️⃣ 💡 Mapa de Ideias (organização mental)

• Mostra relações entre temas e facilita comparações.
• Perfeito para matérias interligadas (História, Matemática, Legislação).
  🕒 Momento ideal: revisão final antes da prova.

✍️ Dica prática: use símbolos para cada tipo

Crie uma marca visual para saber qual tipo de resumo você está lendo:
📖 → conteúdo novo
🧠 → revisão rápida
💡 → conexão de ideias

Assim, durante as revisões, você encontra o material certo sem perder tempo procurando.
Isso transforma seu caderno em uma ferramenta de estudo inteligente, e não apenas em um depósito de anotações. 📒✨

🔄 Como alinhar o tipo de resumo à fase de estudo

📅 Fase 1 – Aprendizado inicial: use resumos de leitura (explicativos).
📅 Fase 2 – Consolidação: transforme em resumos de revisão curtos e objetivos.
📅 Fase 3 – Revisão final: organize tudo em mapas e esquemas interligados.

💬 Exemplo prático:
Ao estudar Razão e Proporção, faça um resumo de leitura com exemplos → depois, um resumo de revisão com fórmulas → e finalize com um mapa conectando Regra de Três, Porcentagem e Escala.

🎓 Mensagem para guardar:

“Resumir sem propósito é desperdiçar tempo.
Mas quando cada resumo tem uma função, ele vira seu guia na jornada da aprovação.” 🚀📘

✍️ 3️⃣ O erro de não revisar o próprio resumo

Esse é o erro que destrói o esforço de horas de estudo: fazer o resumo e nunca mais olhar para ele. 📄💤
Muitos alunos escrevem páginas e páginas com dedicação, mas deixam o material “morrer” dentro do caderno ou da pasta digital.
O verdadeiro poder do resumo não está em escrevê-lo, e sim em revisitá-lo, reler, questionar e aprimorar o conteúdo até que se torne parte de você. 🧠🔥

🎯 Escrever é só metade do processo

A primeira etapa é o registro, mas a segunda — e mais importante — é a revisão ativa.
O resumo é uma ferramenta viva: precisa ser lido, ajustado e enriquecido conforme seu entendimento evolui.

💡 Pense assim:

O resumo que você faz hoje representa o que entendeu hoje.
Se você revisá-lo amanhã, ele pode — e deve — ficar melhor.

Cada revisão transforma o conteúdo escrito em conhecimento consolidado.

🔁 A importância de reler e atualizar seus resumos

Revisar o próprio resumo é uma forma de dialogar com o seu eu do passado.
Você percebe o quanto aprendeu, o que ainda confunde e onde precisa reforçar.

📘 Benefícios da revisão contínua:
✅ Evita o esquecimento precoce.
✅ Aumenta a retenção de longo prazo.
✅ Mostra lacunas de raciocínio.
✅ Melhora a clareza e a síntese das próximas anotações.

🧩 Estratégia prática: A Revisão em 3 Etapas

Essa técnica simples garante que você não desperdice o valor do seu próprio resumo.

1️⃣ Etapa 1 – No mesmo dia:
Revise o resumo logo após escrevê-lo. Faça correções rápidas e acrescente exemplos.

2️⃣ Etapa 2 – Depois de 7 dias:
Releia com calma. Substitua trechos longos por palavras-chave e destaque fórmulas ou conceitos importantes.

3️⃣ Etapa 3 – Após 15 dias:
Transforme seu resumo em material ativo:

• Crie perguntas a partir dos tópicos.
• Monte flashcards com base nele.
• Explique em voz alta usando o conteúdo resumido.

🔁 Cada nova leitura deve ser diferente da anterior — revisar é reescrever com mais clareza.

🃏 Como usar resumos como base para flashcards e autoexplicações

Um bom resumo é uma mina de ouro para criar ferramentas de revisão rápida:
🃏 Flashcards: transforme os subtítulos em perguntas e as respostas em frases curtas.
🗣️ Autoexplicação: tente explicar cada item do resumo sem olhar — se travar, revise aquele ponto.

💬 Exemplo:
Resumo → “Lei de Hooke: F = k × x.”
Flashcard → “Qual é a relação entre força e deformação na Lei de Hooke?”

Assim, o resumo se torna um ponto de partida para treinar a recordação ativa.

⏳ Dica bônus: combine com o ciclo 1-7-15-30

Integre a revisão de resumos à rotina de estudo:
📅 1 dia após o estudo → leitura leve do resumo.
📅 7 dias → revisão com flashcards.
📅 15 dias → explicação oral.
📅 30 dias → mini-simulado com base no tema.

💡 Isso mantém o conteúdo vivo na memória e evita o esquecimento natural.

🎓 Mensagem para guardar:

“Resumo que não é revisado, é conteúdo esquecido.” 🧠💭

Escrever ajuda a entender.
Revisar é o que faz lembrar.
E quem revisa com propósito transforma anotações em conhecimento permanente. 🔁

🎨 4️⃣ O erro de não usar elementos visuais

Um dos motivos pelos quais muitos resumos não funcionam é que eles são monótonos e visualmente cansativos. 😩📝
Um texto sem cores, destaques ou organização visual faz o cérebro trabalhar mais para identificar o que é importante, tornando a revisão demorada e pouco eficiente.
O segredo? Usar o poder da memória visual para transformar o conteúdo em algo fácil de enxergar, lembrar e revisar. 👁️🧠✨

🌈 A mente lembra o que vê, não o que lê

Nosso cérebro é naturalmente visual — ele processa imagens 60 mil vezes mais rápido que textos.
Quando você adiciona cores, símbolos e setas, está ajudando sua mente a criar conexões visuais entre ideias.
Cada cor ou ícone vira uma “âncora” que facilita a lembrança durante a prova.

💡 Exemplo:

• Em vez de um resumo todo em preto e branco: “As leis de Newton explicam o movimento dos corpos e suas interações.”
• Use um visual com cor e estrutura:
  🟥 1ª Lei: Inércia
  🟩 2ª Lei: F = m × a
  🟦 3ª Lei: Ação e reação

Agora o conteúdo se transforma em uma imagem mental organizada.

🎯 Como aplicar elementos visuais nos resumos

Você não precisa ser artista — basta ser intencional.
Veja como deixar seus resumos muito mais eficazes:

🖊️ 1️⃣ Cores estratégicas:

• Azul → conceitos e definições.
• Verde → exemplos e aplicações.
• Vermelho → alertas, fórmulas e pegadinhas.
• Amarelo → observações e curiosidades.

💡 Dica: use sempre as mesmas cores para cada categoria. Isso cria um padrão de reconhecimento automático.

📐 2️⃣ Setas, ícones e balões:
Use ➡️ para indicar causa e efeito, 🔁 para ciclos, ⚡ para pontos-chave.
Esses símbolos ajudam o cérebro a entender a estrutura lógica do conteúdo.

🗺️ 3️⃣ Blocos, quadros e esquemas:
Separe temas em caixas, linhas e tópicos curtos.
Isso cria um visual limpo, ideal para revisões rápidas antes da prova.

🧩 Combine resumos com mapas mentais

Se o conteúdo for grande, transforme o resumo em um mapa mental colorido.

• Coloque o tema central no meio.
• Crie ramificações com conceitos e exemplos.
• Use ícones, setas e destaques.

🎨 Dica prática: ao revisar, cubra partes do mapa e tente lembrar o que estava ali — é revisão visual + ativa ao mesmo tempo!

📱 Ferramentas digitais para resumos visuais

Quer digitalizar sua organização? Experimente:

• 🧠 Canva: ideal para criar resumos coloridos e diagramas.
• 🗺️ XMind: ótimo para mapas mentais e conexões entre temas.
• 📘 Notion: para integrar texto, cores e links de forma inteligente.
• 💻 Miro: excelente para estudos colaborativos e revisões em grupo.

Essas plataformas permitem salvar seus resumos e revisá-los em qualquer lugar — até no celular, durante deslocamentos.

✨ O poder do visual na revisão

Durante a prova, o cérebro não lembra frases — ele lembra imagens.
A cor, o formato e o símbolo que você usou viram gatilhos de memória.
Um aluno visualmente organizado revisa mais rápido e mantém a calma, porque tudo parece familiar na mente.

🎓 Mensagem para guardar:

“Um bom resumo se lê com os olhos e se entende com a mente.” 🎨🧠

Cores e formas não são enfeites — são ferramentas de memória.
Quando o conteúdo ganha vida visual, o conhecimento fica muito mais difícil de esquecer. 🌈📚

🧠 5️⃣ O erro de não transformar o resumo em aprendizado ativo

Um erro fatal entre estudantes é achar que resumir é o suficiente para aprender.
Mas o resumo, por si só, não ensina — ele prepara o terreno para o aprendizado ativo. 🌱📘
O verdadeiro ganho vem quando você pega o que escreveu e começa a interagir com ele, testando, explicando e transformando suas anotações em ferramentas práticas de memorização.

🎯 Resumir é o ponto de partida, não a linha de chegada

O resumo deve ser um instrumento de ação, não um arquivo bonito esquecido na gaveta.
Ele só se torna eficiente quando você o usa para se desafiar, revisar e criar conexões.

💬 Pense assim:

Copiar = absorver.
Resumir = compreender.
Praticar = dominar.

Você precisa passar por todas as etapas — e o resumo deve te conduzir até a última.

🔁 Transforme o resumo em perguntas

Pegue o conteúdo do seu resumo e converta em perguntas que o cérebro precise responder.
Esse é o princípio da recordação ativa, que ajuda a consolidar a memória.

📘 Exemplo:
Resumo → “A fotossíntese transforma energia solar em energia química.”
Pergunta → “Qual processo converte energia solar em química?”

💡 Dica: cubra partes do seu resumo e tente lembrar as respostas — isso força o cérebro a buscar o conhecimento, e não apenas reconhecê-lo.

🃏 Use o resumo como base para flashcards

Se você já resumiu, metade do trabalho dos flashcards está pronta!
Pegue os principais tópicos do resumo e crie cartões de pergunta e resposta.

🃏 Frente → “O que é uma PA (Progressão Aritmética)?”
🔁 Verso → “Sequência com diferença constante entre os termos.”

Esses cartões são perfeitos para revisões curtas — e podem ser lidos em qualquer lugar.
A cada vez que você tenta responder, reforça as conexões mentais criadas pelo resumo.

🗣️ Explique o resumo em voz alta (autoexplicação)

Nada fixa mais o conteúdo do que ensinar o que você acabou de estudar.
Pegue seu resumo e tente explicá-lo como se desse uma aula para alguém.
Se travar, é sinal de que ainda há brechas na sua compreensão.

💬 Método Feynman:
Explique de forma tão simples que até uma criança entenderia.
Quando conseguir fazer isso, você realmente dominou o tema.

📱 Dica prática: grave áudios explicando o conteúdo e ouça durante deslocamentos. Isso transforma o tempo ocioso em revisão inteligente. 🎧

🧩 Crie exercícios baseados no seu resumo

Outro passo poderoso é transformar teoria em prática.
Pegue os conceitos principais e invente pequenos exercícios sobre eles.

📗 Exemplo:
Resumo → “Porcentagem = (parte ÷ total) × 100.”
Atividade → “Se 30 é 15% de um número, qual é o total?”

Resolver o que você mesmo criou ativa a autonomia cognitiva — o cérebro aprende que sabe pensar e resolver, não só repetir.

🚀 Integre o resumo à rotina de revisão

Combine o uso dos resumos com técnicas que aumentam a fixação:
⏱️ Pomodoro: use um ciclo (25×5) só para revisar resumos antigos.
📅 Revisão cíclica: reveja em 1, 7, 15 e 30 dias.
🧠 Aprendizado ativo: questione, explique e resolva questões com base neles.

Com o tempo, você perceberá que não precisa reler tudo — só revisitar os pontos que realmente exigem reforço.

🎓 Mensagem para guardar:

“Resumo parado é conhecimento adormecido.
Resumo ativo é conhecimento em movimento.” 🔁💪

O segredo não está em escrever mais, e sim em usar o que escreveu para pensar, falar e praticar.
Assim, o conteúdo deixa de ser apenas informação — e se transforma em sabedoria aplicada. 🧠🔥

📅 6️⃣ Como revisar com resumos inteligentes

Fazer um bom resumo é apenas o primeiro passo — o verdadeiro diferencial está em como você revisa o que escreveu. 🔁📘
Um resumo inteligente é aquele que trabalha por você: ajuda a lembrar, economiza tempo e reforça os pontos mais importantes sem precisar reler tudo de novo.
O segredo é revisar com estratégia, não por quantidade. 💡⏱️

🧠 O propósito da revisão inteligente

A revisão não serve apenas para “relembrar o conteúdo”, mas para reforçar as conexões neurais e evitar o esquecimento natural.
Cada vez que você revisa, o cérebro entende:

“Isso é importante. Preciso guardar por mais tempo.” 🧩✨

Por isso, quanto mais ativo e espaçado for o contato com o resumo, melhor será a fixação a longo prazo.

⏳ A técnica do ciclo 1–7–15–30

Essa é uma das formas mais eficazes de revisão usada por concurseiros e estudantes de alto desempenho:

📆 Dia 1: reveja o resumo logo após estudar — correções rápidas e reforço inicial.
📆 Dia 7: releia com calma e adicione observações, exemplos ou esquemas visuais.
📆 Dia 15: faça uma revisão ativa — cubra partes do conteúdo e tente explicar sem olhar.
📆 Dia 30: use o resumo como base para resolver questões e testar o que realmente ficou.

🔁 Esse ciclo ativa a curva de esquecimento inversa: quanto mais você revisa, mais lento o cérebro “apaga” a informação.

🃏 Combine resumos com flashcards e autoexplicação

Se quiser potencializar o aprendizado, una ferramentas:

• Transforme o resumo em flashcards curtos com perguntas e respostas.
• Faça uma autoexplicação oral a partir das anotações.
• Use o resumo como base para revisões rápidas de 10 minutos com cronômetro Pomodoro. 🍅

💬 Exemplo prático:

Estude um tema (PA e PG), revise com flashcards no 7º dia e explique em voz alta no 15º.
Assim, o cérebro revisita o mesmo conteúdo de formas diferentes — verbal, visual e lógica — o que triplica a retenção.

📊 Use marcadores visuais e sinalizações

A revisão inteligente é também visual e seletiva:
🔵 Azul → o que você já domina.
🟡 Amarelo → o que ainda precisa reforçar.
🔴 Vermelho → o que errou em provas ou simulados.

Esse sistema de cores cria um mapa visual de progresso, tornando a revisão mais objetiva e motivadora.

⏱️ Integre a revisão aos ciclos Pomodoro

Combine 25 minutos de foco com 5 de pausa, usando cada Pomodoro para revisar apenas um resumo temático.

• 1º Pomodoro → leitura rápida.
• 2º Pomodoro → perguntas e explicações.
• 3º Pomodoro → resolução de questões relacionadas.

Dessa forma, em apenas 1h30 você consegue revisar com qualidade e sem sobrecarga mental.

📚 Crie um “Banco de Revisões”

Mantenha seus resumos organizados por tema e data.
Use etiquetas (Ex.: “Revisado em 7 dias”, “Próxima revisão 15/10”).
Isso transforma seu material em um sistema de aprendizado cíclico — cada resumo tem seu próprio cronograma de reaparecimento.

💡 Dica bônus:
Digitalize seus resumos e guarde-os no Google Drive, Notion ou OneNote para revisar em qualquer lugar, até no celular. 📱✨

🎓 Mensagem para guardar:

“Revisar é o ato de conversar com o que você aprendeu.” 💬📘

Um resumo inteligente é revisado, colorido, explicado e testado.
Ele não serve só para lembrar — serve para consolidar.

Quem revisa com propósito não decora fórmulas: domina ideias. 🔁🧠🔥

🚀 7️⃣ Transforme seus resumos em sua arma secreta para aprovação

Chega de estudar no modo automático. Chega de resumos que só servem para ocupar cadernos e pastas digitais. 📚🔥
O verdadeiro resumo é aquele que te aproxima da aprovação, porque ele não é uma cópia — é uma criação.
É o momento em que você pega o conteúdo e o transforma em algo seu, do seu jeito, com suas palavras e sua lógica.

🎯 O resumo é o espelho da sua mente

Cada resumo revela como você pensa, entende e conecta as ideias.
Não existe “resumo perfeito” — existe resumo funcional, aquele que faz sentido pra você.
Quanto mais autoral, mais eficiente. ✍️💡

💬 Pense assim:

“O resumo não é o fim do estudo.
É o início da sua autonomia.”

Quando você entende isso, estudar deixa de ser uma obrigação e se torna uma construção.

🧠 De aluno passivo a protagonista

Fazer bons resumos é assumir o controle da sua aprendizagem.
É parar de ser apenas um receptor e se tornar o autor da sua própria compreensão.
Cada palavra escrita com intenção cria uma trilha neural — uma ponte entre o conhecimento e a memória duradoura.

📘 Quer um segredo dos aprovados?
Eles não fazem resumos para “guardar o conteúdo”.
Eles fazem resumos para dialogar com o conteúdo.

⚙️ O ciclo do aprendizado ativo

O poder do resumo está em fazer ele circular:
1️⃣ Você estuda.
2️⃣ Resume com propósito.
3️⃣ Revisa com estratégia.
4️⃣ Explica e aplica.
5️⃣ Volta e melhora o que escreveu.

Esse ciclo simples transforma um papel cheio de palavras em uma arma de retenção poderosa.
A cada volta, você aprende mais — e esquece menos. 🔁📈

💬 Exemplo real

Um aluno da “Turma Você Aprovado 2005” contou:

“Passei a revisar meus resumos de Matemática e Português a cada 7 dias.
Em três semanas, comecei a resolver o dobro de questões certas.
Descobri que o problema não era o conteúdo — era a forma como eu estudava.”

Resultado? Ele não decorou. Ele entendeu.
E quem entende, vence. 🏆

🔑 Dicas finais para transformar seu resumo em resultado

📌 Revise sempre com intenção, não por obrigação.
🎨 Use cores e esquemas para visualizar melhor.
🗣️ Explique em voz alta e corrija suas próprias dúvidas.
⏰ Reserve ciclos curtos (Pomodoro) só para revisar resumos antigos.
📊 Atualize seus resumos após cada simulado — eles devem evoluir com você.

💪 Mensagem motivacional da Equipe Você Aprovado 2005:

“O resumo não é só papel — é o reflexo do seu esforço, da sua mente e da sua disciplina.

Quem resume com inteligência, revisa com estratégia e pratica com propósito,
transforma páginas em conquistas e sonhos em aprovação.” 🚀📘🔥

💬 8️⃣ Reflexão final: o poder da síntese

O resumo é muito mais do que um registro — é uma ponte entre teoria e prática, o ponto exato onde o conteúdo deixa de ser abstrato e começa a fazer sentido. 🌉📘
É nesse momento que o aprendizado ganha forma, que o conhecimento passa do papel para a mente, e que cada palavra escrita se transforma em entendimento real.

💭 Aprender a resumir é aprender a pensar

Quando você resume, está organizando ideias, filtrando o essencial e conectando conceitos.
É o mesmo processo que o cérebro usa para raciocinar e resolver problemas.
Por isso, quem domina o poder da síntese aprende mais rápido, lembra por mais tempo e entende com mais profundidade.

📌 Resumir é pensar em voz escrita.
Cada frase que você simplifica é um passo a mais rumo à clareza mental e ao domínio do conteúdo.

✨ Mensagem motivacional da Equipe Você Aprovado 2005:

“Resumo não é o fim do estudo, é o início da compreensão.
Quando você escreve com propósito, transforma informação em sabedoria.” 💡📚

Lembre-se: o poder não está no quanto você anota, mas no quanto você entende.
Continue praticando, revisando e aprimorando —
porque quem aprende a resumir, aprende a conquistar. 🚀🧠